課 題:1、直線上點的投影
2、兩直線的相對位置
3、直角投影定理
課堂類型:講授
教學目的:1、講解直線上點的投影特性
2、講解兩直線各種相對位置(平行、相交、交叉)的投影特點
3、講解用直角投影定理
教學要求:1、理解並掌握直線投影的定比性的解題方法
2、會根據兩直線的投影判斷它們的相對位置,並熟練掌握兩直線平行、相交的作圖問題
3、理解並掌握直角投影定理的特點和解題思路
教學重點:1、兩直線各種相對位置(平行、相交、交叉)的投影特點
2、直角投影定理
教學難點:利用直角投影定理圖解空間幾何問題
教 具:自製的三投影面體系模型
教學方法:例題輔助講解
教學過程:
一、複習舊課
1、三種位置直線(包括七種類型)的投影特性。尤其注意:實長和傾角的判斷。
2、用直角三角形法求一般位置直線的實長及其對各投影面傾角的方法和步驟。
二、引入新課題
上次課我們學習了三種位置直線的投影特性,本次課我們繼續學習空間直線的其他投影特性。
三、教學內容
(一)直線上點的投影
1、直線上點的投影
點在直線上,則點的各個投影必定在該直線的同面投影上,反之,若一個點的各個投影都在直線的同面投影上,則該點必定在直線上。舉例:如圖2-27所示直線AB上有一點C,則C點的三面投影c、c′、c″ 必定分別在該直線AB的同面投影ab、a′ b′、a″b″ 上。
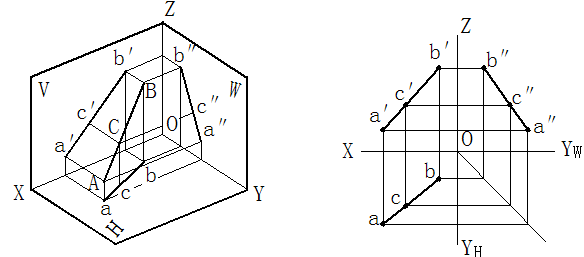
圖2-27 直線上點的投影
2、直線投影的定比性
直線上的點分割線段之比等於其投影之比,這稱為直線投影的定比性。
在圖2-27中,點C在線段AB上,它把線段AB分成AC和CB兩段。根據直線投影的定比性,AC:CB = ac:cb = a′ c′:c′ b′ = a″c″:c″b″ 。
3、講解例題(例2-6) 如圖2-28(a),已知側平線AB的兩投影和直線上K點的正面投影k′,求K點的水平投影k 。

(a)題目 (b) 解法1 (c)解法2
圖2—28 求直線上點的投影
(二)兩直線的相對位置
兩直線的相對位置有平行、相交、交叉三種情況。
1、兩直線平行
(1)特性
若空間兩直線平行,則它們的各同面投影必定互相平行。如圖2-29所示,由於AB∥CD,則必定ab∥cd、 a′ b′∥c′ d′、a″b″∥c″d″ 。反之,若兩直線的各同面投影互相平行,則此兩直線在空間也必定互相平行。
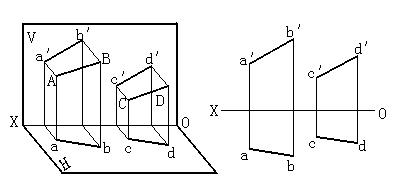
(a) (b)
圖2-29 兩直線平行
(2)判定兩直線是否平行
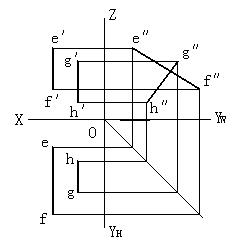
圖2-30 判斷兩直線是否平行
1)如果兩直線處於一般位置時,則只需觀察兩直線中的任何兩組同面投影是否互相平行即可判定。
2)當兩平行直線平行於某一投影面時,則需觀察兩直線在所平行的那個投影面上的投影是否互相平行才能確定。如圖2-30所示,兩直線AB、CD均為側平線,雖然ab∥cd、 a′b′∥c′d′,但不能斷言兩直線平行,還必需求作兩直線的側面投影進行判定,由於圖中所示兩直線的側面投影a″b″ 與c″d″相交,所以可判定直線AB、CD不平行。
2、兩直線相交
(1)特性
若空間兩直線相交,則它們的各同面投影必定相交,且交點符合點的投影規律。如圖2-31所示,兩直線AB、CD相交於K點,因為K點是兩直線的共有點,則此兩直線的各組同面投影的交點 k、 k′、k″ 必定是空間交點K的投影。反之,若兩直線的各同面投影相交,且各組同面投影的交點符合點的投影規律,則此兩直線在空間也必定相交。
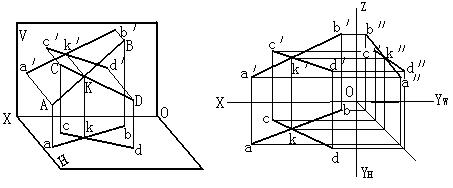
(a) (b)
圖2-31 兩直線相交
(2)判定兩直線是否相交
1)如果兩直線均為一般位置線時,則只需觀察兩直線中的任何兩組同面投影是否相交且交點是否符合點的投影規律即可判定。
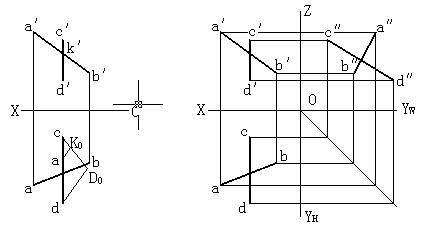
2)當兩直線中有一條直線為投影面平行線時,則需觀察兩直線在該投影面上的投影是否相交且交點是否符合點的投影規律才能確定;或者根據直線投影的定比性進行判斷。如圖2-32所示,兩直線AB、CD兩組同面投影ab與cd、a′ b′ 與c′ d′ 雖然
相交,但經過分析判斷,可判定兩直線在空間不相交。
(a) (b)
圖2-32 兩直線在空間不相交
3、兩直線交叉
兩直線既不平行又不相交,稱為交叉兩直線。
(1)特性
若空間兩直線交叉,則它們的各組同面投影必不同時平行,或者它們的各同面投影雖然相交,但其交點不符合點的投影規律。反之亦然。如圖2-33(a)所示。
(2)判定空間交叉兩直線的相對位置
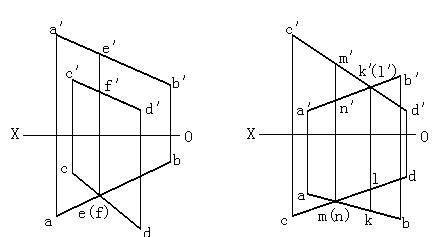
空間交叉兩直線的投影的交點,實際上是空間兩點的投影重合點。利用重影點和可見性,可以很方便地判別兩直線在空間的位置。在圖2-33(b)中,判斷AB和CD的正面重影點k′(l′)的可見性時,由於K、L兩點的水平投影k比l的y坐標值大,所以當從前往後看時,點K可見,點L不可見,由此可判定AB在CD的前方。同理,從上往下看時,點M可見,點N不可見,可判定CD在AB的上方。
(a) (b)
圖2-33 兩直線交叉
(三)直角投影定理
1、概念
空間垂直相交的兩直線,若其中的一直線平行於某投影面時,則在該投影面的投影仍為直角。反之,若相交兩直線在某投影面上的投影為直角,且其中有一直線平行於該投影面時,則該兩直線在空間必互相垂直。這就是直角投影定理。
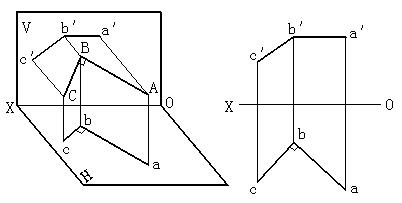
如圖2-34所示。已知AB⊥BC,且AB為正平線,所以ab必垂直於bc 。
(a)
(b)
圖2-34 垂直相交的兩直線的投影
2、講解例題
(目的是幫助學生理解掌握利用直角投影定理圖解空間幾何問題的解題思路和解題方法)
(1)例2-7 求點A到直線BC的距離, 如圖2-35(a)
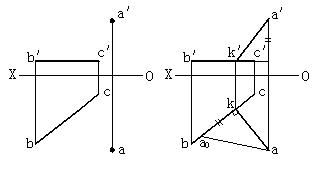
(a)題目 (b)解法
圖2-35 求點到直線的距離
(2)例2-8 如圖2-36(a)所示,已知菱形ABCD的一條對角線AC為一正平線,菱形的一邊AB位於直線AM上,求該菱形的投影圖。
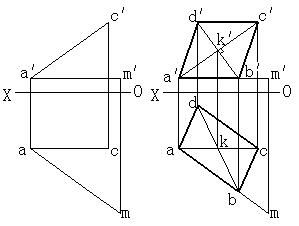
(a)題目 (b)解法
圖2-36 求菱形的投影圖
四、小結
1、平行兩直線的投影特性和判別方法。
2、相交兩直線的投影特性和判別方法。
3、交叉兩直線的投影特性。
4、直角投影定理的應用