第一節 展開原理
1.展開放樣的基本思路
1) 什麼是展開放樣
所謂展開,實際是把一個封閉的空間曲面沿一條特定的線切開后鋪平成一個同樣封閉的平面圖形。它的逆過程,即把平面圖形作成空間曲面,通常叫成形過程。實際生產工作中,往往是先設計空間曲面后再製作該曲面,而這個曲面的製造材料大都是平面板料。因此,用平板做曲面,先要求得相應的平面圖形,即根據曲面的設計參數把平面坯料的圖樣畫出來。這一工藝過程就叫展開放樣。實際工作中,有人把它簡稱為展開,也有人把它簡稱為放樣,本書中採用前者的說法。
2) 展開的基本思路----換面逼近
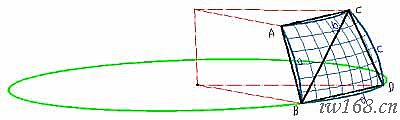
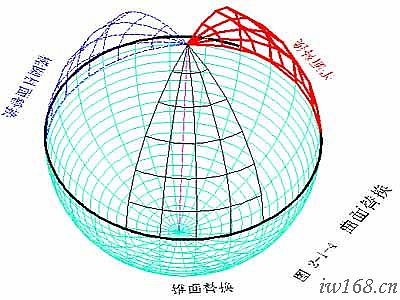
圖2-1-0 換面逼近示意圖
如圖2-1-0,我們按預先設定的經緯網路把曲面網格化,並在曲面上任取其一個四角面元abcd(A、B、C、D為其四個頂點,a、b、c、d為其四條邊界弧線)。連接它的四個頂點A、B、C、D和對角點B、C,將得到一個與四角面元abcd對應的四邊形ABCD以及組成四邊形ABCD的兩個平面三角形△ABC和△BCD。為了簡化我們的研究,我們以三角形△ABC和△BCD代替對應的四角面元abcd,其中直線段AB、AC、CD、DB與a、b、c、d四條弧線分別對應。對所有的網格都做同樣的替代處理,我們就可以得到一個與曲面貼近的,由眾多三角平面元構成的多棱面。多棱面與原曲面當然會存在差別,但是,只要網格數目足夠多,他們的誤差可以足夠小,小到我們允許的公差範圍內。
把曲面換成與之相近、由小平面組成的多棱面,再用多棱面的展開圖去近似替代該曲面的理論展開圖,這就是換面逼近的基本思路。多棱面的展開是容易的,只要在同一平面上把這些小平面元按相鄰位置和共用邊逐個畫出來就得到了多棱面的展開圖。需要指出的是,如何網格化是個中關鍵,這一部分將在講展開方法時詳細介紹。
以上講的是三角平面元替換,其實我們也可以採用其他形狀的小平面來換面逼近。如梯形、六邊形等等。更進一步,我們還可以用簡單曲面,如圓柱面、正錐面等來作類似的替換。實踐證明,這樣的替換逼近效果更好,既簡化了手續,又保證了精度。以下圖例,可資說明。
2.換面逼近的幾個例子
第一個例子是共頂點三角形替換。
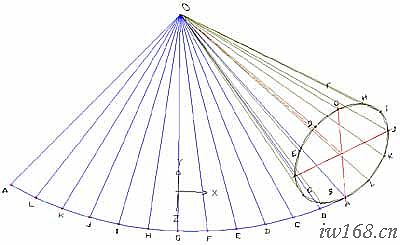
請看圖2-1-1。換面逼近的大致步驟如下:
圖2-2-1 共頂點三角形替換
首先分割:將圓錐底圓分外分為12等分,等分點為A、B、C、D、E、F、G、H、I、J、K、L;然後以過錐頂0與各分點的素線為界線將此圓錐面分為12個共一頂點的三角錐面元;其次換面:用平面三角形△0AB、△0BC、△0CD、…△0KL、△0LA替代對應的三角錐面元;就總體而言,這種替換,也可以理解為用一個12稜錐的外表面來代替圓錐面;然後展開:在同一平面上把這些三角形按照共用邊和共用頂點逐個畫出來,這樣就得到了12個共同一頂點並呈放射狀分佈的三角形組成的平面圖形;我們用這個平面圖形模擬、逼近圓錐的理想展開曲面。當然,這只是一個近似展開圖形,但是他們之間的誤差是可以控制的,例如我們只要增加底圓的等分點數N,其替代誤差隨著N的增加而減小,以至小到允許的公差範圍以內。
以上即所謂共頂點三角形換面逼近。就工藝而言,這是一個可行的方法;從精度來看,關鍵是N的確定,實際中,N根據誤差大小、布點方式、加工工藝和材料性質等因素通過實踐選擇。在各種錐面的展開中,我們都採用這種換面逼近的思路,久而久之,便形成了一個成熟的展開方法。由於它的展開圖線由以頂點為中心呈放射狀布置,我們通常把它叫做放射線展開法。
第二個例子是梯形替換。這是一個用梯形面元替換對應曲面元的例子
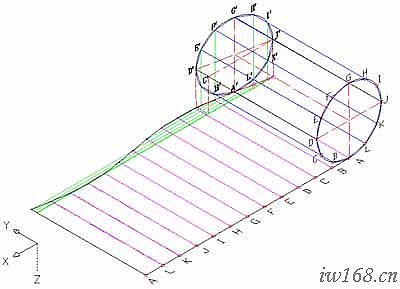
圖2-1-2 梯形替換
如圖2-1-2 所示,本圖系斜口圓柱面展開時進行換面逼近的示意圖。象圓錐面展開的思路一樣,用以取得圓柱微面元的方式仍然是素線分割,但此時的素線已不再相交而是相互平行了。由此得到的微面元是四角曲面,對應的平面圖形是梯形。如圖所示,我們是用梯形AA′BB′去替換四角微面元AA′BB′,逐個替換以後,整個斜口圓柱面的展開將用其內接12邊形為底面的12稜柱面的展開去近似它。
以上即所謂梯形換面逼近。從這個思路出發,在展開放樣中已形成了成熟的平行線展開法。
第三個例子是三角形替換,請看圖圖2-1-3。
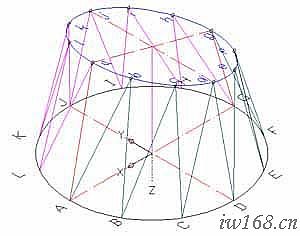
圖2-1-3 三角形替換
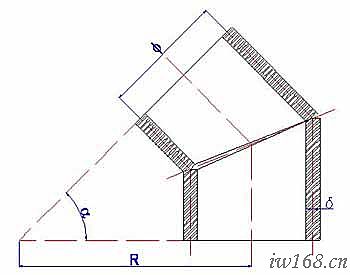
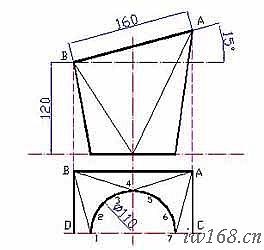
圖中斜口大小頭上下口均為圓,但直徑不同;上口圓中心在下口圓面的投影與下口圓中心同心;此外上下口所在平面之間有15°夾角。需要展開的是以上、下口圓為邊界的周邊蒙面。
本例是這樣換面和逼近的:
首先,將上下口圓分別以對稱中面為基準各自等分為12等分,然後一上一下,依次連接各等分點,由此得到24條直線,即圖中aA、Ab、bB、Bc、cC、Cd、dD…La、aA;
之後分別用每條直線和下口圓心確定的平面分割蒙面,得到24個三角曲面元;同時也得到與之對應的24個平面三角形,即圖中△aAb、△AbB、△bBc、△BcC…△lLa、△LaA;其中12個三角形都有一條邊長度為上口圓周長的1/12,而另外12個三角形都有一條邊長度為下口圓周長的1/12;
為了簡化蒙面的展開,我們再將這24個三角形逐個替換對應的三角曲面元,換言之,我們用一個多棱面來近似大小頭蒙面的展開。這樣替換的結果無疑存在誤差,但它的誤差是可以控制的,例如增大等分點的數目就是減小誤差的途徑,不管你給出的公差多小,總可以設法使誤差不超過你的公差範圍。
最後展開。選定一個切開線,如圖中Aa,並以之作為起始線在同一平面內逐個畫出△aAb、△bAB、△Bbc、△cBC…△lLa、△Ala。這24個三角形共同組成了正確的近似展開圖形。
以上即所謂三角形換面逼近。從這個思路出發,在展開放樣中已形成了成熟的三角形展開法。
第四個例子是曲面替換。(如圖2-1-4)
所謂曲面替換是在換面逼近時,直接用已知的、易展開曲面(如圓柱面、正圓錐面)的曲面元去替代複雜曲面的對應曲面元,以取得更好的逼近效果,從而使複雜曲面的展開工作更簡便,更快捷。
圖2-1-4 曲面替換
本圖以24條經線與24緯線分划球面,得到的曲面元是由相鄰的兩條經線和相鄰的兩條緯線所圍成球面元。對這些曲面元,我們分別進行平面元(梯形面元+三角面元)替換、柱面元替換和錐面元替換。
圖中虛線線部分,採用橢圓柱面元替換。即以一個經線處為原來弧線,緯線處由同一緯線兩端點所連直線,長半徑為球半徑的橢圓柱面元去替代球面元;圖中粗線部分採用了平面替換,即用球面元四個頂點連線組成的梯形替代了球面元,它的四邊都是直線;圖中細線部分則採用了錐面替換,即以一個上下緯線為上下圓的圓錐檯面去替代球面元,這個錐面元的四邊,上下仍為弧線,對應的經線處則已變成了直線;略作比較,不難發現錐面替換、橢圓柱面替換比梯形替換逼近程度高。對於前述的共點三角形替換和梯形替換,我們實際展開中不採用底圓等分點間的弦長而是採用弧長,就是貫徹曲面替換思想的結果。
上述各種換面逼近在整個換面逼近過程中除替換面不同以外,其他情況類似,大同小異,茲不贅述。需要強調的是:實際展開中,對同一曲面的替換面元不必採用同一類型,而是根據曲面的結構特點和簡捷方便的展開原則靈活地混用各種替換面元。
3. 展開放樣的一般過程
設計圖是展開放樣的依據,其表示方式是視圖。眾所周知,視圖上小面元的形狀及其組成線段是實物形狀、實際組成線段在該視圖上的投影,它們的長度不一定反映實際長度。而畫展開圖必須是1:1的實際長度,因此,怎樣通過各視圖上線段的投影去求得線段的實長是展開放樣至關重要的第一步。
求實長常用的方法,一是選擇與實際線段平行、投影反映實長的投影面(先看基本視圖,后選向視圖),在該面視圖上對應量取;二是通過相互關聯的幾個視圖上對應投影之間的函數關係去設法求得。二者可以通過幾何作圖,也可以通過計算求得。
第二步,畫展開圖。展開的重點是畫展開曲線,即展開圖樣的邊線。展開曲線是一般平面曲線,要畫這種曲線,通常先在圖紙上求出曲線上一定數量的、足以反映其整體形狀的點;之後再圓滑連接各點,得出所求曲線“近似版”。此版儘管是近似的,卻可以設法達到事先要求的準確度,因為曲線的準確性跟點的數量有關,越多越准。展開時,為了作圖的方便,點的布置通常採用等分的辦法;在曲線變化急劇的區域,適當插入一些更細的分點,以求得事半功倍的效果。
第二節 展開放樣的基本要求與方法
1.展開三原則
展開三原則是展開時必須遵循的基本要求。
1) 準確精確原則:這裡指的是展開方法正確,展開計算準確,求實長精確,展開圖作圖精確,樣板製作精確。考慮到以後的排料套料、切割下料還可能存在誤差,放樣工序的精確度要求更高,一般誤差≤0.25?。
2) 工藝可行原則:放樣必須熟悉工藝,工藝上必須通得過才行。也就是說,大樣畫得出來還要做的出來,而且要容易做,做起來方便,不能給後續製造添麻煩;中心線、彎曲線、組裝線預留線等以後工序所需的都要在樣板上標明。
3) 經濟實用原則:對一個具體的生產單位而言,理論上正確的並不一定是可操作的,先進的並不一定是可行的,最終的方案一定要根據現有的技術要求、工藝因素、設備條件、外協能力、生產成本、工時工期、人員素質、經費限制等等情況綜合考慮,具體問題具體分析,努力找到經濟可行,簡便快捷、切合實際的經濟實用方案,絕不能超現實,脫離現有工藝系統的製造能力。
2.展開三處理
展開三處理是實際放樣前的技術處理,它根據實際情況,通過作圖、分析、計算來確定展開時的關鍵參數,用以保證製造精度。
1) 板厚處理
上面所說的空間曲面是純數學概念的,沒有厚度,但實際中的這種面只存在於有三度尺寸的板面上。是板料就會有厚度,只不過是厚度有厚有薄而已。板料成形加工時,板材的厚度對放樣有沒有影響?答案是肯定的,不可能沒有影響;板材的厚度越大,影響越大,而且隨著加工工藝的不同,影響也不同。下面先看兩個例子。
⑴ 我們把L×b×δ的一塊鋼條彎曲成曲率為R的圓弧條時,發現上面(弧內側)的長度變短了,下面(弧外側)的長度變長了。根據連續原理,其中間一定存在一個既不伸長也不縮短的層面。這個層面我們叫它中性層。那麼,這個中性層的位置在哪裡呢?實踐證明,中性層的位置跟加工的工藝和彎曲的程度有關。如採用一般的彎曲工藝,當R>8δ時,中性層的位置在板料的中間。這一客觀事實給我們的啟示是:如果設計了這樣一個圓弧條要我們加工,加工前的展開料長應該按中徑上的對應弧段計算。顯然,該圓弧條的展開長度是L。如此類推,倘要用厚度為δ鋼板卷制一個圓筒,其展開長度應按中徑計算,即L=πφ。
這是一個很重要的結論,因為按中徑展開,更準確一點,按中性層展開就是我們鈑厚處理的基本原則。
請注意,圖2-2-1中沒有給出尺寸數值的單位。未標單位不是沒有單位,而是採用默認單位。機械製造行業默認的單位是毫米。圖中長度314沒有標明單位,按默認值,其單位就是毫米。以後均應如此,恕不重述。
設計圖上往往給出的是外徑(φw)或者是內徑(φn),展開時要換算出中徑(φ)。它們之間的關係是:φ=φw-δ=φn+δ
中性層位置,可用下列經驗公式計算。
R0=R+X0δ 式中X0按下表取值:
表2-1 中性層位移係數經驗值
(表中,中性層距裡邊的距離為X0δ,板厚為δ,X0=中性層位移係數)
| R/δ | 0.1 | 0.25 | 0.5 | 1.0 | 1.5 | 2.0 | 3.0 | 4.0 | >4 |
| X0 | 0.28
| 0.32 | 0.37 | 0.42 | 0.44 | 0.455 | 0.47 | 0.475 | 0.5 |
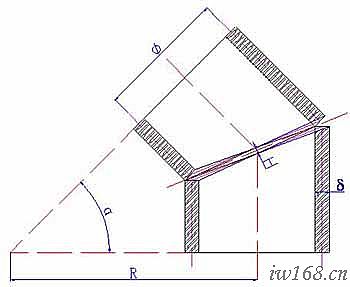
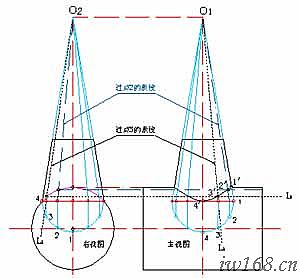
⑴ 再看圖2-2-2,我們來討論厚度對彎頭裝配間隙、角度和彎曲半徑的影響。
已知:直徑φ 管口角度α 管壁厚度δ 彎曲半徑 R
圖2-2-2 厚度對彎頭裝配的影響
一般板料切割時切口垂直於板面。由於厚度的存在,成形后板的內外表面端線不在同一平面,直接影響按端頭裝配時的介面間隙、角度和彎曲半徑。圖中,內半圈管外皮相接、外半圈管里皮相接。此時中間形成空隙,其大小H=2δsin(α/2)。同時由於中徑處存在偏離,不能直接在立面圖中原定位置相接,造成彎曲半徑增大。
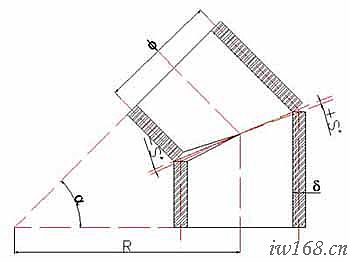
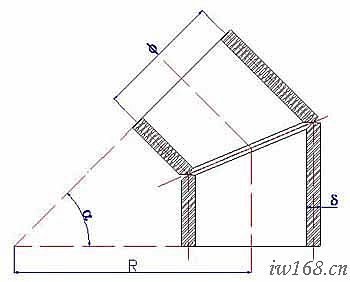
為了避免或減少板厚對彎頭裝配的影響,在彎頭展開時,應先作介面的位置和坡口設計,然後再據此展開放樣。圖2-2-2a中的做法,就是按內半圈外皮相接、外半圈裡皮相接,分別調整內、外半圈的半節角度來保證尺寸、形狀、位置方面的精度要求。這種處理辦法叫角度調整法。而圖2-2-2b中的做法是以中徑斜面為準(斜角為α/2),內外倒坡口來形成正確的介面形狀的(一般應用於厚板),這種處理辦法叫坡口調整法;至於圖2-2-2c中的做法則是以中徑斜面為準(斜角為α/2),將內半圈外皮處、外半圈板里皮處用鎚子錘平或用切割器修平來達到目的的(一般應用於2~6mm薄板),這種處理辦法叫管口修平法。
圖2-2-2a 角度調整法
圖2-2-2b 坡口調整法
圖2-2-2c 管口修平法
2) 介面處理
⑴ 接縫位置
單體接縫位置安排或者是組合件介面的處理看起來無足輕重,實際上是很有講究的。放樣時通常要考慮的因素有:
① 要便於加工組裝;
② 要避免應力集中;
③ 要便於維修;
④ 要保證強度,提高剛度;
⑤ 要使應力分佈對稱,減少焊接變形等。
一般設計圖不給出接縫位置。放樣實踐中,全靠放樣工根據上述原則靈活處理。由這點區區小事,可以看出,光懂點幾何作圖,不懂工藝,不懂規範,不具備一定的機械基礎知識,不經過必須的放樣訓練,是不可能真正做好這項工作的。
⑵ 管口位置
管口位置和接頭方式一般由設計決定。針對這些要求,展開時要具體分析並進行相應的處理。一般的原則是,一要遵循設計要求和有關規範,既要滿足設計要求,也要考慮是否合理;二要考慮採用的工藝和工序,分辨哪些線是展開時畫的還是成形后畫的;三要結合現場,綜合處理,分辨哪些線是展開時畫的還是現場安裝時再畫的。
⑶ 連接方式
是對接還是搭接?是平接還是角接?是接於外表面還是插入內部?是焊接還是鉚接?是普通介面還是加強接頭?這些都是必須了解清楚的,因為連接方式不同,展開時的處理就不同。一旦遇上了對鈑金工藝不很專業的設計人員所設計的接頭和連接方式,展開時的處理就更顯得重要了,因為對一個好的冷作鈑金工,他不但要會按圖施工,而且一旦遇上按圖不宜甚至不能施工時,要拿得出切實可行的修改方案來。
⑷ 坡口方式
為了焊透,厚板焊接需要開坡口。坡口的方式主要跟板厚和焊縫位置有關。設計藍圖即便規定了坡口的形狀樣式,放樣時還是應該畫出1:1的介面詳圖,以便驗證設計的接頭方式是否合理,或者是設計沒有指明時決定合理的接頭方式。
2) 余量處理
余量處理俗稱“加邊”,就是在放出的展開圖某些邊沿加寬一定的“多餘”邊量。這些必要的余量因預留的目的不同而有不同的稱呼,如搭接余量、翻邊余量、包邊余量、咬口余量、加工余量等等。
余量處理的問題在“量”上,到底余多少?留大了增加加工工作量,留少了下道工序沒辦法加工。留是常識,留得合適是水平。這個量,有時圖紙上有標註,更多的時候要放樣者自己把握。如何把握?在實際工作中並不一定是一個計算問題,有時更多是一個實踐問題,需要去“試”,試出一個結果來,往往更靠得住。
舉一個例子。咬口是薄板常用的連接方式,且如今咬口大多用轆骨機成形。咬口余量怎麼取?它跟機器的性能、調整的狀況、板料的長短、操作的方法等,都有關係。因此,余量數據的取得,應該先粗算下料,上機成形,然後測量比較、修正定尺。
3. 展開三方法
1) 幾何法展開
幾何法展開,準確一點,應叫幾何作圖法展開。展開過程中,求實長和畫展開圖都是用幾何作圖的方式來完成的。幾何法展開又可細分為許多實用方法,常用的有三種:
⑴ 放射線法。這種方法在換面逼近時使用的面元是三角形,但這些三角形共一頂點,常用在錐面的展開中。放射線法的一般步驟是:
① 針對某曲面的結構,依照一定的規則,將該曲面劃分為N個共一頂點、彼此相連的三角形微面元;
② 對每個三角形微面元,都用其三頂點組成的平面三角形逐個替代,即用N個三角形替代整個曲面,其替代誤差隨著N的增加而減小;
③ 在同一平面上按同樣的結構和連接規則組合畫出這些呈放射狀分佈的三角形組,從而得到模擬曲面的近似展開圖形;
④ N根據誤差大小、加工工藝和材料性質等因素通過實踐選擇;
⑵ 平行線法。這種方法在換面逼近時使用的面元是梯形,常用在柱面的展開中。平行線法的一般步驟是:
① 針對某曲面的結構,依照一定的規則,將該曲面劃分為N個彼此相連的梯形微面元;
② 對每個梯形微面元,都用其四頂點組成的平面梯形逐個替代,即用N個梯形替代整個曲面,其替代誤差隨著N的增加而減小;
③ 在同一平面上按同樣的結構和連接規則組合畫出這些梯形,於是得到模擬曲面的近似展開圖形;
④ N根據誤差大小、加工工藝和材料性質等因素通過實踐選擇;
⑶ 三角形法。這種方法在換面逼近時使用的面元是三角形,可用於柱面、錐面等各種曲面的展開,應用廣,準確度高;放射線法、平行線法適用的,三角形法,只是作圖手續多一些,工作量相對大一些。三角形法的一般步驟是:
① 針對某曲面的結構,依照一定的規則,將該曲面劃分為N個彼此相連的三角微面元;
② 對每個三角微面元,都用其三頂點組成的平面三角形予以替代,即用N個三角形替代整個曲面,其替代誤差隨著N的增加而減小;
③ 在同一平面上按同樣的結構和連接規則組合畫出這些三角形,於是得到曲面的近似展開圖形;
④ N根據誤差大小、加工工藝和材料性質等因素通過實踐選擇;
關於這些方法,我們將通過以後的實例來促進大家的了解。
1) 計演算法展開
計演算法展開,顧名思義,要通過計算。其實在展開過程中,它只是用計算的方法求實長,畫展開圖還是用幾何作圖。怎麼計算?如何弄清楚展開曲線兩坐標變數之間的函數關係?一般鈑金製品的曲面是由基本曲面組成的,而基本曲面在立體解析幾何中都確切地給出了解析式。由這些聯立方程組可以求出空間相貫線的聯立方程組,進而求得選定面上的相貫線方程和實長方程,於是展開曲線上預設各點的坐標就能一一計算出來。這種通過解析方程來進行展開計算的方法也叫解析法展開。它當然歸屬於計演算法,限於篇幅,此處就不多講了。
展開實踐中還有一種表格法,亦稱查表法,即按項目、參數事先計算好數據,列成表格,使用時查表取數求得實長,再去畫展開圖。這種方法不過是計演算法的演化,無須分列。
2) 計算機輔助展開
計算機在鈑金設計製造中的應用之一即是計算機輔助展開和計算機輔助切割,在數控切割機上,二者甚至可以同時完成。計算機輔助展開的應用軟體不少,多以薄鈑件設計為主,兼有展開功能;方法上則分參數建模和特徵造型兩大類;應用中各有特色,尤其是電子電氣的薄殼箱體製作,精彩到美崙美奐的地步。
對於大型綱結構、厚板製件,計算機輔助展開仍然走的是傳統展開的路子,計算展開圖中的各項數據,展開畫圖。其中,在電腦上用幾何法展開,快捷精確,數據一點就來,效果很好。顯然,在今後的鈑金製造中,CAD、CAE、CAM、CAPP將大行於世,因為它們不僅是完美的助手,而且是創新的平台。
但它仍在發展之中,也有不盡人意之處。如數控激光切割,切割頭的角度還不能數控;切割頭活動的範圍有限;機位固定,不適於流動作業;它的價格不菲,尚未普及等等。
正是上述原因,我們這次展開放樣訓練,選擇的是比較直觀的傳統幾何法模式。
4. 常用三樣板
1) 樣板的應用與分類
為了避免損傷鋼板,我們一般不在鋼板上直接放樣,而是通過放樣,製作樣板,再靠准樣板去鋼板上畫線。這樣做的好處一是避免把展開放樣時的諸多輔助線和中心點都劃在或打在鋼板上,造成鋼板表面損傷;二是樣板重複使用,在多件製作時的優越性更明顯,而且藉助樣板我們可以在鋼板上套料排圖,能使材料得到充分利用。
放樣時一般要做三個樣板。除了下料用的展開樣板外,還有成形時檢測彎曲程度的成形樣板和組裝時檢測相對角度、相互位置的組裝樣板。這兩種樣板通常又叫作卡樣板。
2) 外包樣板、內鋪樣板與平料樣板
樣板因使用場合的不同而有不同的形式,常用的有外包樣板、內置樣板與平料樣板。平料樣板用得最多,此前我們提到的樣板都是成形前的平料樣板。但有時候我們需要在成形后的鈑料上畫線,這時就要用到外包樣板或內鋪樣板了。管外畫線,用外包樣板;筒內畫線,用內鋪樣板。如製作直徑不很大等徑焊接彎頭,工藝上宜先卷製成管子,后切割成管段,再組焊彎頭,這種情況下就要準備外包樣板。而在大管大罐內畫線開孔那就要用內鋪樣板。
特別指出的是:平料樣板號料,彎曲的是板料,板厚處理考慮的是板料厚度;外包樣板和內鋪樣板號料,彎曲的是樣板,板厚處理考慮的是樣板的厚度。
3) 樣板的材料與製作
製作樣板的材料常用的有厚紙板、油毛氈和薄鐵皮。這些材料各有其長,根據需要選用:厚紙板性價比小,適宜作小樣板;油毛氈拼接方便,適宜畫大的展開圖,應用廣泛,但不能多次使用;薄鐵皮做的樣板儘管價格偏高,但強度與剛度都好,精確耐用,便於保存,特別適於批量生產,更是作卡樣板的首選材料。
第三節 幾何法展開的三個基本方法與典型實例
一、幾何作圖
1. 常用幾何劃線工具
說起畫線,大家沒有不明白的.然而提到劃線,能準確表述的人就不多了。此處所說的劃線是專業術語,它也是一種畫線,只不過用的工具和畫的對象不同。劃線是用高硬度劃線工具,如划針、划規、中心沖,直接在材料上精確刻劃和沖點,劃出的線條很細。為了凸顯它,往往還要沿線打上樣沖眼;為清晰起見,必要時金屬材料表面還應該專門塗色。顯然,划針劃線比鉛筆畫線要精確得多。展開放樣和樣板製作的材料一般採用薄鋼板、厚紙板和油毛氈,在這些材料上精確作圖,以劃為主;當然,需要時也還是要用色筆畫的,只要能保證精度要求,什麼便當,就用什麼畫。以下介紹的,是鈑金冷作工以劃為主的常用劃線工具。
1) 15m盤尺、3m捲尺、1m長尺、300?鋼尺、150?鋼尺、150?寬座角尺、大三角板、吊墜
2) 划規、分規、地規、划針、划針盤、石筆、粉線、墨斗
3) 中心沖、手錘
4) 展開平台
2. 常用幾何畫線
對展開放樣來說,以下常用的一些幾何畫線是必須掌握的。因時間關係,這裡只提出基本要求,具體的畫法就不多講了。不清楚的地方,請自己複習《工程製圖》中的相關內容。
1) 長直線、大圓弧的畫法
2) 特殊角度、一般角度的畫法
3) 直線、圓弧、角度的等分
4) 直線曲線的吻接
5) 常見曲線的畫法(正弦曲線、橢圓、四心圓、擺線、漸開線、阿基米德螺線)
二、大小頭與放射線法
1.大小頭的表面特性
大小頭上下口平行,是圓管變徑時使用的連接件,有同心和偏心之分。同心大小頭表面是正圓錐面,偏心大小頭表面是斜圓錐面。立管變徑時,連接件常採用同心大小頭。水平管路變徑,要求嚴格時用同心大小頭就不合適了。這是因為介質為液體時水平管路需要排除內部產生的、妨礙運行的氣體,因此連接處要求管道頂平,以利於排盡不需要的氣體;相反,氣管則需要排除積液,管路要求底平,以利於排盡不需要的液體。90°偏心大小頭,它可以在水平敷設的管路變徑時使管道頂平或者是底平,因而在水平管路變徑中大顯身手。
前面說過,同心大小頭是正圓錐面,偏心大小頭是斜圓錐面,它們有什麼共同點呢?我們不妨設想一下:水平面上有一個圓D(圓心為O),水平面外有一個點A,有一條直線L通過該點和圓上一點。現在讓這條直線一端固定在A點不動,另一端沿著圓的軌跡向同一個方向轉動一周,於是這條線在空間將劃出了一個曲面,這個曲面就是錐面。如果固定點在通過圓心的鉛垂線上,形成的錐面就是正圓錐面;如果固定點不在通過圓心的鉛垂線上,則所形成的錐面是斜圓錐面。
形成錐面的那條線叫母線,母線運動的軌跡圓叫基線,基線所在的水平面叫基面。母線在轉動中通過的的每個位置都形成一條特定的直線,這些線,我們稱之為素線。如果母線不通過固定點,而是保持與基面的某一軸向成一固定角度,也沿某一給定基線運動,那麼劃出來的曲面就是柱面。其中母線垂直於基面、基線為圓時的特別例子,就是我們非常之熟悉的正圓柱面。
這種母線是直線而形成的曲面,就是所謂直紋面。直紋面由無數素線組成。錐面的素線相交,柱面的素線平行。就展開而言,這個認知很重要,前者引申出了展開的放射線法,後者引申出了展開的平行線法。
直紋面的展開比較好處理,成形時大多是繞素線彎曲,因而製造起來比較容易。從方便製造、經濟合理方面考慮,一般殼體設計,大都選擇各種直紋面的組合。
2.同心大小頭的展開
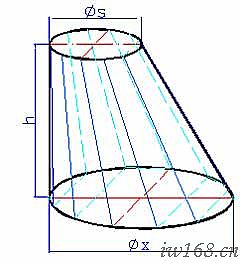
同心大小頭的展開其實在小學數學課本就已經講過,只是現在印象淡漠了。用得太少,記不住是正常的。現在我們靜下心來,仔細看看圖2-3-0,慢慢回憶起它的展開過程。
1) 已知條件:大頭中徑 φD=120; 小頭中徑 φX=60; 高 h=100; 大、小口平面互相平行,且小頭圓心在大頭平面的投影與大頭圓心重合。
2) 展開步驟:
⑴ 以水平面為大頭基面,根據已知條件作立面圖,即作HS⊥SA,其中HS=h, SA=φD /2;過H作HB∥SA,HB=φX/2;
⑵ 將錐台斜邊AB延長與中軸線HS的延長線交於O;以O為圓心,以OA、OB為半徑分別畫弧;
⑶ 在OA弧上量取AD弧,使其弧長等於底圓周長(L=πφD);
⑷ 連OD,交OB弧與C;則扇形ABCD為所求展開圖形。
3) 注意:不宜先在OB弧上量取小頭圓周長。因為OB弧上的量取誤差將在外弧(OA弧)上出現誤差放大,可能導致超出允許的公差範圍。
4) 也可以通過計算展開扇形的圓心角來確定OD。圓心角可按下式計算:
將本題已知條件代入,α=103.4°
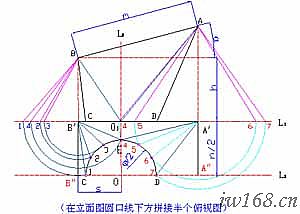
5) 如圖2-3-0,在AA′下方拼畫半個俯視圖,將底圓6等分並過等分點畫出素線;對展開圖亦作同樣等分並過等分點畫出素線;不難看出,他們之間存在著曲面元和平面元、曲面弧長和平面弧長之間的一一對應、等量轉換的關係。這種處理方法,我們在以後的展開中將時常用到。
圖-3-0 同心大小頭的展開圖
3.偏心大小頭的展開
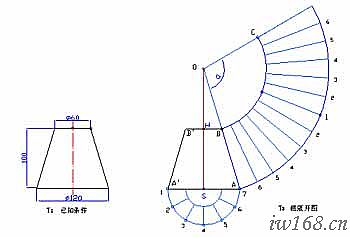
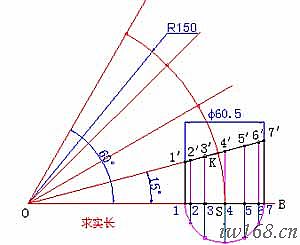
偏心大小頭的展開稍許複雜點,但與同心大小頭一樣,它也可以通過大頭斜錐削掉小頭斜錐而得出來,因此,偏心大小頭的展開問題實質上是斜錐的展開問題。斜錐的展開程序,首先是按已知條件畫出立面圖,然後確定底圓等分點,再求各等分點素線的實長。怎麼求?請看圖2-3-1a:
圖2-3-1a 斜錐的已知條件與實長分析 圖2-3-1b 斜錐展開的第一步---求實長
1) 已知條件:
大頭中徑 φX 小頭中徑 φS
斜錐台高 h 偏心距 e 斜錐台上下口面平行且關於中面0S7對稱
2) 展開分析:
⑴ 在△0S6中,0S(點劃線)是斜錐的高,S6(虛線)是素線06(粗線)在俯視圖上的投影。因為0S垂直於底面,故△0S6是直角三角形;∠0S6為直角;而素線06是該直角三角形的斜邊。這就是我們求斜錐素線實長的依據。
⑵ 錐台實際上是以同一斜錐切掉上面小錐形成的,顯然,展開圖組成上也有同樣關係。展開時我們先處理大錐,后解決小錐。
現在著手斜錐展開的第一步,求斜錐底圓各等分點上素線的實長。請看圖2-3-1b。
3) 按已知條件畫立面圖、俯視圖。注意:畫立面圖時,應以中徑為準。如果已知條件給定的是外徑或中徑,就必須根據板厚先求出中徑。
⑴ 畫水平線L1並在其上取點O1,E,使O1E=e;然後以O1為圓心,φX /2為半徑畫半圓,交水平線L1於1、7二點;
⑵ 過E作水平線L1的垂線L3並在其上取O2,使O2E=h;過O2作水平線L2;以O2為圓心,φS/2為半徑畫弧,交L2於1°、7°二點;
⑶ 連1、1°,7、7°並延長相交於O點;過O點作L1的垂線,垂足為S;過S作半圓的切線。S7、切線與半圓O1實際上構成斜錐的半個俯視圖,所以這一步又叫做“拼接半個俯視圖”。
4) 利用∠OS7為90°,求實長。
為了方便展開,以後我們畫圖時常常幾個視圖疊合畫在一起,這樣,點的標號可能會重複出現,繪圖者自己當然清楚它們所在的視圖;在對稱情況下,作圖一般只畫一半,遇到全圖展開時,對稱點點號都按同號對稱布置。了解這種處理方式,反而好尋找對應點。
⑴ 六等分下口半圓;
⑵ 以錐頂的垂足S為圓心,其到各等分點的長度為半徑畫弧,將各分點素線的投影長度等量轉移到底邊,得點1、2、3、4、5、6、7;連接各轉移點與錐頂,則各轉移點與錐頂的距離就是各分點素線的實長。
⑶ 上述實長線被小口線所截的上邊線段即是小錐對應實長。
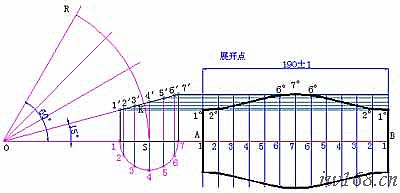
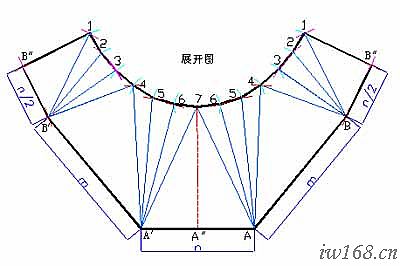
以下進行斜錐展開的第二步,畫展開圖。請看圖2-3-1c。
圖2-3-1c 斜錐展開圖
1) 畫展開圖
⑴ 以01為剖開線,在合適處垂直方向作中線07;
⑵ 以0點為圓心,各分點素線實長為半徑畫得如圖1、2、3、4、5、6弧;
⑶ 以7點為圓心,1/12底圓周長為半徑畫弧,交6弧於二個6點,再以兩6點為圓心,1/12底圓周長為半徑畫弧,交5弧於二個5點;如此下去,同法求至兩個1點;
⑷ 檢查所得13個點的曲線長度,如與計算所得的底圓周長誤差大於3mm,應及時修正;
⑸ 圓滑連接各點得大口展開線;
⑹ 如圖連接0點與各點,並在上述各線上由0點起量取小錐相應實長;圓滑連接所得各點即成小口展開線;
⑺ 連接大、小口對應端點,完成整個展開圖。
斜錐台展開全過程可參考圖2-3-1。
4.放射線展開法
按上述步驟展開的方法叫放射線展開法。放射線法常用於錐形曲面的展開,其展開基本過程是:
1) 針對素線有同一頂點的錐面,根據其結構,依照一定的規則,將該曲面劃分為N個共一頂點、彼此相連的三角微面元;對每個三角曲面元,都用其三頂點組成的平面三角形逐個替代,即用N個三角形替代整個曲面,其替代誤差隨著N的增加而減小;
2) 在同一平面上按同樣的結構和連接規則組合畫出這些呈放射狀分佈的三角形組,逐步得到模擬整個曲面的近似展開圖形;因為共一頂點這些三角形的邊形成一組放射線;
3) 利用這一組放射線我們可以將其他相似的展開曲線、開孔線等畫出來;
4) 確定替代元的數量N是很重要的實際問題,N過大,增大工作量和勞動時間;N太小,精度達不到要求;N一般根據誤差大小、加工工藝和材料性質等因素通過實踐選擇。
三、彎頭的展開與平行線法
1.圓管彎頭及其主要參數
彎頭是用於管路轉彎時的連接件。按口徑,分為等徑彎頭和異徑彎頭;按製作方式,則有彎制、壓制、擠制和焊制之分;按截面形狀,可以分為圓管彎頭、方管彎頭、方圓管轉換彎頭、異徑彎頭(在轉彎過程中截面大小改變而形狀不發生改變)、異形轉換彎頭(截面形狀在轉彎過程中步發生改變)等第。我們這裡講的彎頭展開,指的是一節節組焊而成的“蝦米彎”,主要包括等徑圓彎頭、異徑圓彎頭、方圓管轉換彎頭;其他形狀的彎頭並不常見,因為沒有特殊需要,誰也不會設計這種展開複雜,加工困難的玩意兒來增加成本、自找麻煩。
焊制彎頭的幾個主要參數:(參看圖2-3-2a)
1.彎頭角度:指彎頭兩個管口面間的夾角;
2.彎頭直徑:指彎頭管材的外徑、內徑或中徑;
3.彎曲半徑:指管段軸線的內切圓半徑。即管口中心到了兩管口面交線的距離;
4.彎頭節數:彎頭的端節是中間節的一半,兩個端節合起來是一節,再加上中間節數,合稱彎頭的節數;
關於彎頭節數,目前沒有統一的規定。有的把中間節的數量稱為節數,有的把組成彎頭的段數稱為節數。如圖2-3-2a所示彎頭,前者叫二節彎,後者叫四節彎,我們鈑金冷作工則叫三節彎。稱三節彎的合理之處,一是便於半節角度的計算;二是彎頭的節數等於焊接介面的數量,非常之明了;三是對兩個半節組成的一節彎,前者就納不入自己的系列,要換著名兒叫,後者則根本不存在一節彎頭的概念。
2.平行線法
現在介紹展開時常用的另一個方法---平行線法。平行線展開法常用於素線互相平行的柱形曲面的展開,其展開的基本過程如下:
1) 針對曲面結構特點,依照設定的規則,將該曲面劃分為N個彼此相連的梯形微面域(微面域以下稱面元);梯形的平行邊一般選在曲面的素線處;N一般根據誤差大小、加工工藝和材料性質等因素通過實踐選擇;
2) 對每個梯形微面元,都用其四頂點組成的平面梯形逐個替代,即用N個梯形替代整個曲面,其替代誤差隨著N的增加而減小;
3) 根據視圖的尺寸、位置的對應關係,即:“長對正、高平齊、寬相等”的三等關係和上下、左右、前後的方位關係,用與各視圖相關的平行線求取相貫點的位置、每個梯形各邊的實際長度;
4) 在同一平面上按同樣的結構和連接規則組合畫出這些梯形,於是得到模擬曲面的近似展開圖形。彎頭、三通等柱形表面的展開放樣都是平行線展開法的典型例子。
3.等徑彎頭的展開
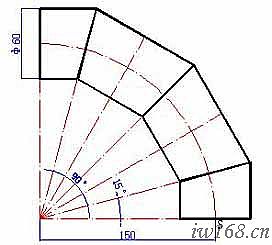
請看圖2-3-2a。
圖2-3-2a 彎頭的已知條件 圖2-3-2b 彎頭實長圖
1.彎頭展開的已知條件與要求
1) 已知條件
彎頭角度 α=90°; 管子外徑 φW=60; 彎曲半徑 r=15; 彎頭節數 n=3; 樣板厚度 δ=0.5
2) 展開要求
① 用平行線法作外徑φ60管的外包全節樣板。
② 方法正確:(展開方法不是唯一的,本題要求按教師指定的方法做)
③ 作圖精確:幾何作圖誤差≤0.25,展開長度誤差≤±1。
3) 展開準備
① 求半節角度:按節數計算半節(端頭)截面傾斜角度;(αb =α/2n)
② 展開三處理:按管徑、材料板厚、連接方式和製作工藝決定展開中徑、介面位置和余量。
因為是外包樣板,畫立面圖時,管口直徑應該選擇包在管外的樣板捲筒的中徑。本題已知條件中給出了管子外徑,實際上就是給出了樣板捲筒的內徑。故樣板捲筒的中徑φ=60+0.5=60.5。
2.求實長:
見上圖2-3-2b。
1) 畫半節彎頭端面角度線:
⑴ 先計算半節彎頭端面角度;
αb=α/2n=90°/(2´3)=15°
⑵ 作水平直線OB,在OB上取OS=150;分別以O、S為圓心,OS為半徑畫弧交於R;
⑶ 4等份弧SR,得等分點K,連OK並適度延長。
2) 畫半節彎頭立面圖:
⑴ 先計算外包樣板筒半徑 R=f/2=(60+0.5)/2=30.25(可通過四等分長度為121的線段獲取);
⑵ 在OB線的S點兩側取1、7兩點,使S1=S7=30.25
⑶ 過1、7作OB的垂線11′、77′,交OK於1′、7′;梯形(11′7′7)即是半節彎頭立面圖。
3) 求實長:
⑴ 以S為圓心,S1為半徑在下方畫半圓並6等分之;
⑵ 過各等分點作OB的垂線,交OB為1、2、3、4、5、6、7;交OK為1′、2′、3′、4′、5′、6′、7′;則11′、22′、33′、44′、55′、66′、77′為半節彎頭管口各分點上的素線實長。
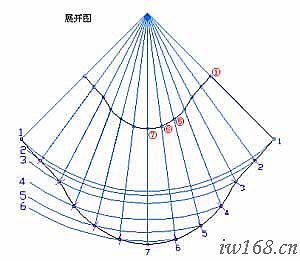
3.畫展開圖:
見圖2-3-2c。
⑴ 計算展開長度:L=p(60+0.5)=190
⑵ 作平行素線組:在OB上取AB=190(注意誤差控制在%%p1以內),12等分AB;過各分點作AB的垂線組,上下長度略超過77′;以11′為切開線,依次標明各分點;
⑶ 求埠展開曲線:從1′~7′引SB的平行線,與對應垂線交於1°、2°、3°、4°5°、6°、7°,圓滑連接這13個點,此即半節埠的展開曲線;曲線梯形(AB1°7°1°)為半節(端節)的展開圖形。
⑷ 畫全節展開圖:以AB線為中軸線畫出上述展開曲線的對稱曲線。這兩條關於AB對稱的展開曲線及其對應端點連線所圍成的區域就是展開圖。
實際操作時,一般用划規量取各點實長值,尺寸大時則直接用尺量取。再以AB上各對應分點為中心上下划弧或量取實長,以求展開點;然後將這些展開點圓滑連接成展開曲線。連線時可以用曲線板或彎曲的鋼尺,也可以手工描。用曲線板或彎曲的鋼尺時,一次畫線至少要通過三點;手工描時,可以先把各點用直線連成折線,然後折線的基礎上根據曲線的凹凸方向適度修描;為避免接縫處產生尖角,此處曲線要修描到其切線與接縫垂直。
必要時,下料的鋼板上還須畫出折彎線,作為成型時彎曲加工的位置。這些線就是平行素線組。因此平行素線組在樣板上還應該保留下來。
圖2-3-2c 彎頭展開圖
4、直管號料
小口徑彎頭一般直接用小口徑管製作,不需要卷管,所以樣板要做成外包式的,包著管子畫線。至於大口徑管,市面沒有現成管材供應,只能卷制。但是由於單節彎頭寬度尺寸變化大,上機卷制時弧度彎曲不均勻,因此工藝上常採用先卷管后割端節的做法,這也需要製作外包樣板。樣板製作好了以後,怎樣要它去號料呢?
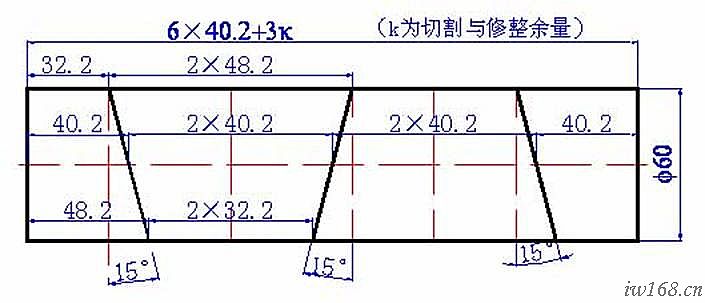
1) 首先要計算準直管管長
三節彎頭由兩個全節和兩個半節組成,畫線時不要數量不符,少則誤工,多則浪費。尤其是,不要忘記了留切割和修整余量。由圖中量得半節中心高為41.2,則直管長度L=6×41.2+3k。(k為切割與修整余量,其值根據精度要求、切割方法和操作水平綜合選取)
2) 下料時應先在管端圓周四等分處沿軸向畫出四條素線,作為外包樣板對位時的基準線,並按事先計算的數據標出定位點;
3) 按基準點線用樣板畫線,有誤差要分析,及時調整糾正;
4) 各基準線處也是彎頭組裝時的重要的對位點,為了防止工作中所畫線被檫掉,最好在基準線處打上幾點樣沖眼或作上其他標記。
等徑三節彎頭展開全過程可參考圖2-3-2。
圖2-3-2d 直管號料圖
四、相貫線
1.相貫線的概念
相貫線是空間曲面之交,是兩個面方程的公共解。相貫線是空間曲線,由於實際應用中都採用視圖來傳遞設計加工信息,因而圖紙上顯示的相貫線通常是它的投影曲線。以後,我們常說的相貫線,指的都是空間相貫線對某個面的投影線,而其本身反倒很少提及,一旦提起,還特別點明。
由於投影是二維的平面曲線,它垂直於投影面方向上的特性因取定值而被忽略,但它反映在其他視圖上,根據三視圖長、寬、高方面的尺寸關係和前後、上下、左右方面的位置關係我們可以把它找回來;其他二向所具備的關係和特徵則不因其為投影而完全喪失,研究其平面特性正是我們展開放樣的必經之路。
研究相貫線的作用。歸納起來有二點:
⑴ 設計、繪圖的需要;
⑵ 用於展開放樣。(主要是通過展開點求實長和藉助相貫線求實長)
2.相貫線的畫法
要畫相貫線先找相貫線上的點,這些點我們稱之為相貫點,將相貫點圓滑連接成線,並把這線當作相貫線。顯然,這裡存在誤差,但是我們有辦法使誤差足夠的小,小到你允許的範圍以內,這就不失為一個實用的好辦法。這種關鍵的相貫點找的越多,畫線的精度越高。因此可知,要解決畫相貫線的問題,重要的是解決找相貫點的問題。
有時候,求得的展開點直接對應於等分點,由此通過相貫點完全可以求得實長了,展開線已沒有畫出來的必要。如果相貫體中的一個通過等分求得相貫點,而對另一個,這些相貫點根本不具有等距性質,不便測量,不便於展開。這時候我們可以先通過容易求的相貫點,畫出相貫線;再等分另一個並通過前面得出的相貫線來確定等分點上素線的實長,繼而畫出展開圖。這種做法也是展開實踐中經常循用的方法。
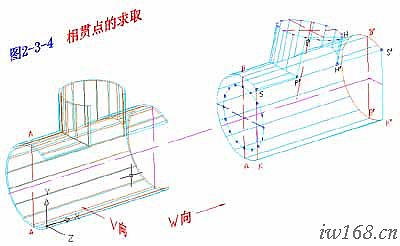
3.相貫點的求取
眾所皆知,視圖中的相貫線是一個二元函數,求相貫點必須對其中一個變數賦值。怎麼取值?定步長取值,即按等差級數取值是公認的首選。從幾何角度看,賦值問題其實就是相貫點的布點問題,此前用過的等分圓的作法就是基於這個思路。展開放樣,動輒等分圓。為什麼?因為等分圓的最大好處在於方便操作,這意味著校準了圓規的針距以後可以多次使用,而校準針距是很費時間的事。因此,展開實踐中,大都採用等分待展開面來布置所求相貫點。
鑒於展開曲線並非線性的,在不同的等分區間變化不一樣,布點時我們常採用改進的等分法,即插值等分法。在曲線急劇變化段,適當插入幾個等分點參與展開,以精細刻畫該段的曲線變化。
布點的另一個要求,一定要有關鍵點、極限點,如上下方向的最高點、最低點,左右方向的兩個邊點等等。倘若原來的布點方案實施中發現局部考慮不足,還要及時補點。
等分數N的選定有講究,一是其大小,根據精度要求和曲線變化確定;二是其性質,必須從操作方便考慮,一般取N=2i3j (式中:i=(0,1);j=(2,3,…);理由是3等分半圓,2等分弧容易操作。倘若你讓N取了13、37之類的質數,那就麻煩了。每等份長度T≈5~10%,(基本尺寸大時取小值,基本尺寸小時取大值)關於相貫點的求取,下面我們結合幾個例子說明常用的一些方法。
⑴ 視圖法:
視圖法從三個視圖的內在關係(尺寸、位置)入手,通過三視圖之間的三等關係和方位關係,在同一視圖上畫出每個相貫曲面具備這種關係的點的位置線;從這些位置線的交點去求出相貫點。視圖法主要應用於關鍵點、極限點的求取上。
⑵ 素線法:
二個直紋面相貫,相貫點是這兩個曲面的公共點。從分析相貫點所具有某一特徵的入手,在同一個視圖上分別畫出兩個曲面上具有該點特徵的二條素線,其交點就是相貫點。這種求相貫點的方法叫素線法。圖2-3-4a中,在立面圖上通過支管端圓等分點P(點P與中面ABB′A′的距離為h)作支管素線PP′, 然後在側視圖的主管表面上找到與中面ABB′A′的距離為h的點S並過S轉向立面圖上作主管素線SS′,兩素線PP′與SS′的交點P′即為相貫點。圖中等分點H與P到中面的距離一樣,過H的素線HH′與SS′的交點H′為另一相貫點。
圖2-3-4a 素線法求相貫點(1)
又如圖2-3-4b中正錐面與圓柱面相貫,為了求得某一等分點3對應的相貫點3′的位置,我們先在主視圖錐面上畫出該點所在的素線L1;然後畫出側視圖上的素線L1,L1與圓柱面的交點就是3′點在側視圖中的位置;由此向主視圖畫圓柱面軸線的平行線L2,則L1、L2的交點K就是所求相貫點。
圖2-3-4b 素線法求相貫點
⑶ 軌跡法:
軌跡法從點所具有某種特性的入手,通過三視圖之間的關係,在同一視圖上畫出每個相貫曲面具有該特性的點的軌跡;從這些對應軌跡的交點去求出相貫點。例如通過到中面等距離點的軌跡求異徑斜三通的相貫點;又如通過到兩中軸交點等距離的點的軌跡求錐-管相貫、錐-錐相貫時的相貫點。
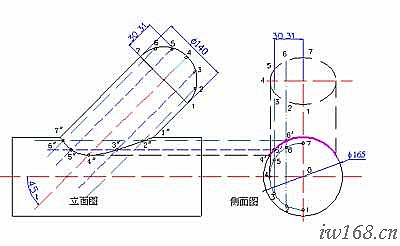
圖2-3-5中的兩異徑管相貫,就是利用距中面等距離的點的軌跡來求相貫點的。
圖2-3-5 軌跡法求相貫點
主視圖中,從支管點5畫出的虛線平行於支管軸線,這線即支管表面距中面距離等於30.31的點的軌跡;在側視圖中,設法求出相貫線上距中面距離也等於30.31的5′點,再過此點向立面圖作主管軸線的平行線,此線即主管表面距中面距離等於30.31的點的軌跡;兩軌跡的交點5″就是立面圖上所求的相貫點。
1.已知條件:支管外徑f140;主管外徑f165;軸線相交且夾角45°
2.求作:在立面圖畫出兩管的相貫線
3.分析:要畫相貫線,先求線上的關鍵點,然後連點成線,點越多越準確。本題相貫點的求得,可通過畫出主管、支管表面距中面17等距離點的軌跡並求其交點的辦法進行。
4.步驟:
⑴ 先在立面圖上過支管端圓各等分點畫支管軸線的平行線,這些線就是與各等分點距中面17等距離的點的軌跡;
⑵ 之後按各等分點到中面的距離,在側視圖兩管相貫線上找該點的對應位置。相貫線就在側視圖主管外圓上由支管邊線界定的弧段,圖中用粗線顯示;
⑶ 過各找到的點引主管軸線的平行線與支管平行線組相交,找出並標明對應交點。
⑷ 圓滑連接上述各點,即得立面圖上的兩管相貫線。
⑷ 輔助截面法:
輔助截面法採用一組截面去截兩個相貫曲面或者採用二組截面分別對應截兩個曲面,從截得的截線入手求相貫點。它依據相貫曲面的某一特徵選取截面組,通過三視圖之間的關係,在同一視圖上畫出每個相貫曲面上的截線,對應截線的的交點即為所求相貫點。請注意,這裡的截面概念並不獨指平面,而是已拓廣到了曲面。截面的選取是有條件的,它截得的截線必須是簡單易畫的直線、圓弧,而不能是又要通過求許多點才能畫出的複雜曲線。
常用的截面組有平行平面組、旋轉平面組和同心球面組。平行平面組一般用於柱面、錐面、球面等迴轉面,平行基面根據截線是否簡單易畫來確定;旋轉平面組共一個轉軸,一般用於錐面迴轉面,軸線多在迴轉軸線或錐頂連線;同心球面組則用於軸線相交的錐面、柱面和其他迴轉面,中心在軸線交點。例如布置與兩軸線構成的中面平行的一組平行平面組求異徑斜三通的相貫點;又如通過到兩中軸交點布置同心球面求錐-管相貫、錐-錐相貫時的相貫點。
細心的讀者會發現,前面所講的素線法、軌跡法其實不過是輔助截面法中的一個小類,例如素線法採用了平行平面組或旋轉平面組(參考圖2-5-1~圖2-5-6);而軌跡法中,通過到中面等距離點的軌跡求異徑斜三通的相貫點就是採用平行平面組的輔助平面法;通過到兩中軸交點等距離的點的軌跡求錐-管相貫、錐-錐相貫時的相貫點就是採用同心球面組的輔助球面法。在掌握素線法、軌跡法的基礎上,全面理解和用活輔助截面法將使你在展開技術上提高一個層次。因此,輔助截面法的掌握與運用,可以作為展開放樣技能考核的鑒定點。
五、三通的展開
1. 三通及其主要參數
三通是管路引出一個分支管時的連接件。如果在一個連接件上同時引出二個支管,那就是四通了。這裡我們只介紹三通,因為只要會做三通,用同樣的方法再做一個支管不就成了四通!支管與主管口徑相同時的三通叫等徑三通,口徑不同時則叫異徑三通;支管中心線與主管中心線相交,交角為90°叫正三通,否則叫斜三通;如果中心線不相交,那就叫偏三通;還有,支管與主管截面形狀都不同的三通叫異形三通。列出這麼些三通的目的不僅是提出一個分類名稱,還想告訴大家:從展開和製造的角度看,加工時它們一個比一個難。因為課時的限制,本次實訓的重點只能放在難度不大的圓管三通製作上。
圓管三通的主要參數有:三通的角度;主管、支管的直徑;支管對主管的偏心距;其他相關大小尺寸。圓管三通的展開與圓管彎頭一樣採用平行線法展開。對數理基礎較好的學生來說,展開的難度不在於展開方法的掌握,而在於精確作圖的操作功夫。從這一個例題開始,我們應該把關注的重心轉移到幾何畫圖的技能訓練上來,不但要知道怎麼畫,還要熟練、精確和迅速地畫好展開圖。
2. 等徑斜三通的展開
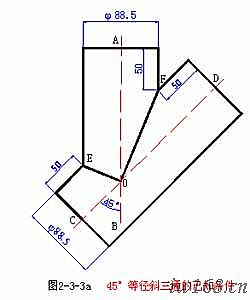
請看圖2-3-3a。
1) 已知條件
如圖2-3-3a所示:主管外徑 j88.5 支管外徑 j88.5 中心線夾角 45° 樣板厚度 0.5 主、支管管端到開口的最段距離均為50
2) 展開要求
⑴ 求作支管的外包樣板和主管的開孔樣板;
⑵ 方法正確;(按照指定的平行線法展開)
⑶ 作圖精確。(作圖精度≤0.5,展開長度≤±1,展開曲線連接圓滑,線寬<0.5)
3) 展開分析
⑴ 本題兩等徑管相貫,中心線相交;正因為等徑,故其相貫線不能偏向任何一方,因此在立面圖中相貫線只能是中心線夾角的平分線;
⑵ 從圖中∠A0B 和∠A0D看支管,其實就是兩個不同角度彎頭裡邊的一半,因此支管的展開跟彎頭的展開方法是一樣的;
⑶ 展開曲線應該是相位相差180°的兩個半波正弦曲線相連而成。
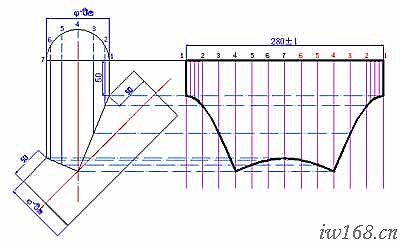
圖2-3-3b 斜三通支管展開圖
4) 求實長
見圖2-3-3b。
⑴ 按外包樣板捲筒中徑畫支管立面圖;
⑵ 配畫支管半個截面園並6等分該半圓;
⑶ 求支管各等分點處素線實長。
5) 畫支管展開圖
⑴ 按展開長度(89π)和等份數(12)作平行線組;
⑵ 按相應實長在對應平行線上取展開點;
⑶ 圓滑連接各點並完成展開圖。
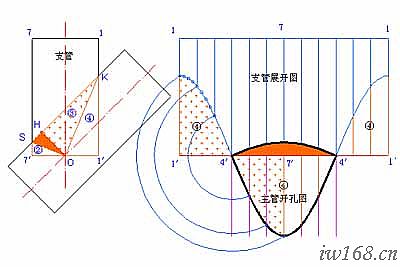
圖2-3-3c 斜三通主管開孔展開圖
6) 畫主管開孔展開圖
見圖2-3-3c。
⑴ 連SK,過O點作SK的垂線,垂足為H;OH將OSK劃分為塊①、塊③兩部分,這就意味著,主管開孔的展開圖是由塊①和塊③的展開圖組成的;
⑵ 在過O點、支管軸線的垂線上截取7、1兩點,兩點與O點的距離等於支管半徑;連1、1′與7、7′,得到一個與支管等高的短管;
分析:由立面圖可見,如果把短管11′77′去掉塊②、塊④兩塊,就是支管。而因等徑的緣故,塊①與塊②,塊③與塊④是完全相等的,這也意味著,主管開孔的展開圖可以由塊②和塊④的展開圖組成;再看展開圖,在塊②下面把塊④按圖示位置拼上,即得到主管開孔的展開圖。
上述開孔展開的方法給我們提供了一個利用前一個圖中的展開曲線畫后一個展開圖的途徑。需要提醒的是,這種小竅門僅在等徑時有效,因為只有這時候塊①與塊②、塊③與塊④才存在相等的關係,才有置換的可能。
⑶ 在支管展開圖上,以兩個4點為中心對稱點將兩個半塊④相對逆向旋轉180°,即得主管開孔展開圖。
本題在展開中還對等分點的布點問題做了些簡化處理。為了細緻反映曲線急劇變化段(1-2)、(2-1)的形狀,可以在這二段間插入6個48等分點,並將求得相應實長用於展開。這樣,我們在12等分的基礎上只增加6個點就接近了48等分的精度。這種簡化的插點法在展開中時常應用。
45°等徑斜三通展開全過程可參考圖2-3-3。
3.異徑斜三通的展開
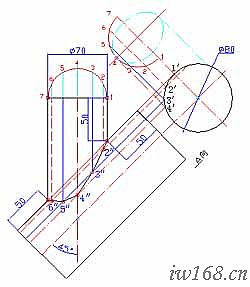
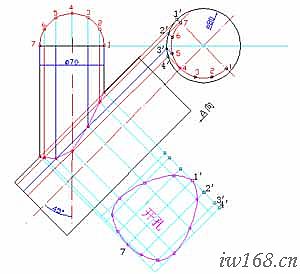
1) 已知條件與要求
⑴ 已知條件:支管外徑f70;主管外徑f80;軸線相交且夾角45°;中面上的相貫點到管端距離均為50;兩軸線所在面為對稱中面;
⑵ 製作斜三通上插管的外包樣板和主管的開孔樣板;
⑶ 分析:本題的關鍵是畫立面圖上兩管的相貫線。要畫相貫線,先求線上的關鍵點,然後連點成線。相貫點的求得,我們用前面學過的軌跡法或來解決,即通過畫出主管、支管表面距中面17等距離點的軌跡並求其交點的辦法進行。支管的展開和主管開孔的展開與等徑三通展開,因方法雷同,過程類似,因而只作概要陳述。
圖2-3-7a 異徑斜三通的相貫線 圖2-3-7b 異徑斜三通主管開孔展開圖
2) 求相貫點:
⑴ 以垂直方向為支管軸線方向,畫三通立面圖和A向視圖(主管軸向圖);作圖時支管直徑取樣板捲筒中徑,主管外徑不變。
⑵ 在支管上拼畫俯視方向的半個截面圓並6等分之;然後畫過各等分點的素線;這些線就是支管上與各等分點到中面(17)等距離的點的軌跡;
⑶ 之後在A向視圖上按對應等分點到中面的距離作中面的平行線,該平行線與兩管相貫線的交點即為主管上的等距點。(A向相貫線就在A向視圖主管外圓上,圖中以粗線顯示)
⑷ 過等距點作主管軸線的平行線,即得立面圖主管上到中面等距離點的軌跡;該線與支管對應等距線的交點就是所求的相貫點。同法求得與7個等分點對應的7個相貫點。
⑸ 圓滑連接上述各相貫點,即得立面圖上的兩相貫線。(單就支管展開而言,本題求得相貫點即可,不必畫出相貫線)
3) 插管展開:
⑴ 根據插管各等分點素線與對應主管等距線的交點求實長;
⑵ 按展開長度和等份數作平行線組;
⑶ 按相應實長在平行線上取定展開點;
⑷ 圓滑連接各展開點並完成展開圖。
4) 開孔展開圖:
⑴ 以1″7″為對稱中線,依次以主管正截面上各等距點之間的弧線長度(直接在弧上測量取值)為間距畫與主管軸線平行的平行線組;
⑵ 過各相貫點作主管軸線的垂直線並與上述平行線組中的對應線相交求展開點;
⑶ 圓滑連接各展開點,完成展開圖。
異徑斜三通展開全過程可參考圖2-3-7。
六 方圓頭的展開與三角形法
1.方圓頭的結構特點
方圓頭是連接圓管與方管的連接件。一般我們把大的一頭叫地,小的一頭叫天,因而方圓頭有時叫”天方地圓”,有時候叫”天園地方”。分析一下方圓頭的結構,我們發現它總是由平面部分和斜錐面部分組成的,平面部分都是三角形,斜錐部分則是4個1/4斜錐。
方圓頭展開看起來複雜,實際上道理比較簡單,只不過是一個前面學過的斜錐展開而已。展開的關鍵在於弄清錐頂所在點,然後向圓所在面投影。方圓頭平口時等高,實長只跟俯視圖投影而變;方圓頭有一個對稱面時,要展開2~3個斜錐;方圓頭有二個對稱面時,只要展開一個斜錐。畫展開圖時,不要顛倒了頂點,直線邊組成折線相連,都是直線;弧線邊弧弧相連,全部曲線。
方圓頭的主要參數有:方口的對邊尺寸m×n;圓口的中徑Φ;指定點高度h;兩個端面之間的夾角;偏心距;板厚。
2.三角形法
方圓頭的展開我們採用三角形展開法。三角形法比放射線法、平行線法適用範圍更廣,只是作圖手續多一些,工作量大一些。三角形展開法的基本程序是:
1) 針對某曲面的結構,依照一定的規則,將該曲面劃分為N個彼此相連的三角微面域;
2) 對每個三角微面元,都用其三頂點組成的平面三角形予以替代,即用N個三角形替代整個曲面,其替代誤差隨著N的增加而減小;
3) 在同一平面上按同樣的結構和連接規則組合畫出這些三角形,於是得到曲面的近似展開圖形;
4) N根據誤差大小、加工工藝和材料性質等因素通過實踐選擇。
3.方圓頭的展開
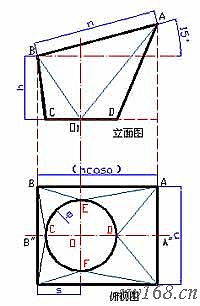
請看圖2-3-8a。
圖-3-8a 方圓頭的已知條件 圖2-3-8b方圓頭展開實長圖
1) 已知條件與展開要求
⑴ 天圓--中徑 j ; 地方--邊長(對邊中距)m×n ; 小錐高度 k; 上下口面夾角a;
⑵ 該天圓地方有一個對稱中面,點(B在圓面的投影)對圓中心的相對位置為(-s,n/2);
⑶ 求作該天園地方的展開下料樣板。
2) 畫立面圖
如圖2-3-8b。
⑴ 作水平線L1及其垂直線BB′,B′為垂足,且BB′=h;
⑵ 過B作與水平線夾角為a的直線BA,且BA=m;再過A作L1的垂線,交L1於A¢;
⑶ 在L1下方作與其距離為n/2的水平線L2;
⑷ 在BB¢右側作與其距離為s的平行線L3,交L1、L2於O1、O;
⑸ 在O1兩側取與其距離為j/2的C、D兩點;連B、C、D、A和B、O1,A、O1,完成立面圖。
3) 畫俯視圖
實際展開時不必畫出了整個俯視圖,只須在B′A′處拼畫半個俯視圖就可以了。
⑴ 延長BB′、AA′交L2於B²、A²,連B′、B″,A′、A″;
⑵ 以O為圓心、j/2為半徑作半圓,交L2於C、D,交L3於E;
⑶ 在俯視圖上連CB′、EB′、EA′、DA′完成俯視圖。
4) 求實長
⑴ 等分半圓口,分點為1、2、3、4、5、6、7,其中4與E為同一點;
⑵ 以B¢、A¢為圓心,將B¢至1、2、3、4,A′至4、5、6、7的長度轉移到L1上去求實長;
⑶ 連B與B′A′線上的各對應點,得B錐各分點素線實長,即B1、B2、B3、B4;同法求得A錐各分點素線實長,即A4、A5、A6、A7。
5) 畫展開圖
⑴ 算圓口12等份弧長:s=;
⑵ 以B1線為剖切線,7A″為對稱中心線畫展開圖。分別以A、A′為圓心、A7為半徑畫弧,
交於7點;連A、A、7三點;
⑶ 如圖所示,以A、A′為圓心,6A、5A、4A為半徑畫弧,畫時注意控制弧長及位置;
⑷ 以7為圓心,s為半徑畫弧,交A6弧、A′6弧於兩個點6;然後分別以兩個點6為圓心、s為半徑畫弧,交A5弧、A′5弧於兩個點5;之後再以兩個點5為圓心、s為半徑畫弧,交A4弧、A′4弧於兩個點4;
⑸ 分別以點4為圓心、B4為半徑畫弧和以A點為圓心、m為半徑畫弧,得兩弧交點B;同法在另一邊可求得B′;
⑹ 分別以B、B′為圓心,B3、B2、B1為半徑畫弧;
⑺ 以兩個點4為圓心、s為半徑畫弧,交B3弧於兩個點3,同法繼續求得兩個點2和兩個點1;至此我們共求得圓口展開曲線上的13個點;
⑻ 沿這13個點量其長度,如其累積誤差≤±3mm,則圓滑連接該13點,得到圓口展開曲線;
⑼ 以兩個點1為圓心、BC長為半徑畫弧,與以B、B′為圓心、n/2為半徑所畫弧相交,得左右兩個B″;連1、B″、B、A和1、B″、B′、A,完成整個展開圖。
具體的展開全過程,還可以看圖2-3-8方圓頭的展開畫法,也可以參考圖2-4-4天方地圓的展開練習和圖2-4-5、圖2-4-6天圓地方的展開練習。
圖2-3-8 方圓頭的展開圖
第四節 【實訓項目一】:展開放樣訓練
練習1. 按圖2-4-1a已知條件製作偏心大小頭的下料樣板
1.已知:
底圓中徑 φx=100+k;(k為學號的后兩位數) 頂圓中徑 φs=0.5φx;
大小頭高 h=120; 斜錐頂點在底面上的投影位於底圓上;
2.求作該偏心大小頭的展開樣板
3.展開圖畫法見圖2-4-1。
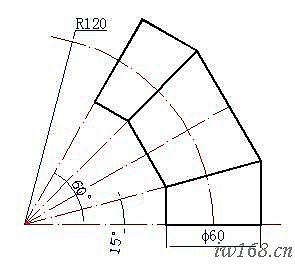
練習2. 按圖2-4-2a的已知條件製作等徑60°兩節彎頭的全節外包樣板。
1. 已知:
彎頭角度 a=60°; 彎頭節數 n=2; 彎曲半徑 R=120;
被包管外徑 φ=60; 樣板厚度 d=0.6;
2. 求作上述φ60管彎頭的外包樣板;
3. 展開圖畫法見圖2-4-2。
圖2-4-1a 偏心大小頭的已知條件 圖2-4-2a 兩節彎頭的已知條件
練習3. 按圖2-4-3a等徑斜三通的已知條件製作插管的外包樣板和主管的開孔樣板
1.已知:
斜角α=60°; 管外徑ф=60; 樣板厚度δ=0.5; 插管短邊L=50;
2.求作插管外包樣板與主管開孔樣板;
3.展開圖畫法見圖2-4-3。
練習4. 按圖2-4-5天圓地方的已知條件製作下料平樣板
1.已知:
圓口中徑 f=120; 方口對邊中距 m×n=150×150;
中心高 h=120; 傾斜角 a=15°; 板厚 d=1
該方圓頭有一個對稱面,且對方口平面投影時,天圓圓心投影與方口中心重合。
2.求作該天圓地方的展開樣板。
3.本題展開方法見圖2-4-5。
練習5. 按圖2-4-6a斜底天方地圓的已知條件製作下料平樣板
1.已知:
天圓 Φ=110; 地方 L=160×160; 小錐高 h=120; 傾斜角 α=15°; 板厚 d=1;
該方圓頭有一個對稱面,且對圓 口平面投影時,方口中心投影與圓心重合;
2.此題畫立面圖時應注意與上題區別。上題頂圓中心在方口平面的投影與方口中心重合;本題方口中心在圓口平面的投影與圓心重合;
3.展開畫法可參考圖2-4-6。
圖2-4-5a 天圓地方的已知條件 圖2-4-6a 斜底天圓地方已知條件
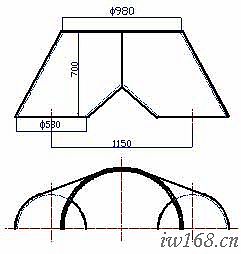
練習7. 按圖2-4-7平口漸縮三通的已知條件製作下料平樣板
1.已知:
上下口平行,距離h=700; 兩下口中心距L=1150; 上口中徑f980;
下口中徑f580; 板厚d=6。
2.要求用計算機輔助繪製該漸縮三通的展開圖。
3.說明:
⑴本題實質是兩斜錐相貫,上口各等分點對應的實長線被相貫線所截取的線段即是實長。
⑵為簡便計,右圖中俯視圖只畫一半。
4.展開畫法參考圖2-4-7
圖2-4-7 平口漸縮三通的已知條件