流體動力潤滑理論的基本方程是流體膜壓力分佈的微分方程。它是從粘性流體動力學的基本方程出發，作了一些假設條件后得出的，這些假設條件是：流體為牛頓流體；流體膜中流體的流動是層流；忽略壓力對流體粘度的影響；略去慣性力及重力的影響；認為流體不可壓縮；流體膜中的壓力沿膜厚方向不變。
下圖中，兩平板被潤滑油隔開，設板A沿x軸方向以速度v移動；另一板B為靜止。再假定油在兩平板間沿 z軸方向沒有流動(可視此運動副在z軸方向的尺寸為無限大)。現從層流運動的油膜中取一微單元體進行分析。
由圖可見，作用在此微單元體右面和左面的壓力分別為p及
,作用在單元體上,下兩面的切應力分別為τ及
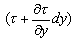。根據x方向的平衡條件,得
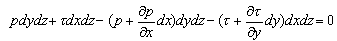
整理后得
根據牛頓流體摩擦定律,得
，代入上式得 
該式表示了壓力沿x 軸方向的變化與速度沿y軸方向的變化關係。
下面進一步介紹流體動力潤滑理論的基本方程。
1、油層的速度分佈
將上式改寫成
（a）
對y 積分后得
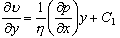
（b）
（c）
根據邊界條件決定積分常數C1及C2:當y=0時,v= V; y=h(h為相應於所取單元體處的油膜厚度)時,v=0,則得
代入（c）式后,即得
（d）
由上可見,v由兩部分組成：式中前一項表示速度呈線性分佈，這是直接由剪切流引起的；后一項表示速度呈拋物線分佈，這是由油流沿x方向的變化所產生的壓力流所引起的。
2、潤滑油流量
當無側漏時,潤滑油在單位時間內流經任意截面上單位寬度面積的流量為
（e）
將式(d)代入式(e)並積分后,得
（f）
設在 p=pmax處的油膜厚度為h0(即
時，h=h0),在該截面處的流量為
（g）
當潤滑油連續流動時,各截面的流量相等,由此得 
整理后得
該式為一維雷諾方程。它是計算流體動力潤滑滑動軸承(簡稱流體動壓軸承)的基本方程。可以看出,油膜壓力的變化與潤滑油的粘度、表面滑動速度和油膜厚度及其變化有關。經積分后可求出油膜的承載能力。由雷諾方程及圖示的壓力分佈也可以看出,在h>h0段,速度分佈曲線呈凹形，
，即壓力沿x方向逐漸增大；而在h，壓力沿x方向逐漸降低。在其間必有一處的油流速度變化規律不變，此處
，其壓力 p 達到最大值。由於油膜沿著x方向各處的油壓都大於入口和出口的油壓，因而能承受一定的外載荷。 由上可知,形成流體動力潤滑(即形成動力油膜)的必要條件是：
相對運動的兩表面間必須形成收斂的楔形間隙。 被油膜分開的兩表面必須有一定的相對滑動速度，運動方向為使油從大口流進,小口流出。 潤滑油必須有一定的粘度，供油要充分。
