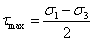1、材料力學的任務:
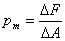 (1.1)
(1.1)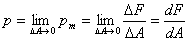 (1.2)
(1.2) 表示。
表示。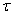 表示。
表示。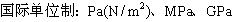
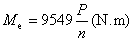
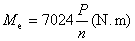
 ,且為平均分佈,其計算公式為
,且為平均分佈,其計算公式為 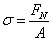 (3-1)
(3-1)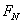 為該橫截面的軸力,A為橫截面面積。
為該橫截面的軸力,A為橫截面面積。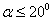 時
時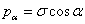 (3-2)
(3-2)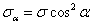 (3-3)
(3-3)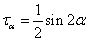 (3-4)
(3-4) 為橫截面上的應力。
為橫截面上的應力。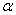 由橫截面外法線轉至斜截面的外法線,逆時針轉向為正,反之為負。
由橫截面外法線轉至斜截面的外法線,逆時針轉向為正,反之為負。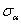 拉應力為正,壓應力為負。
拉應力為正,壓應力為負。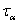 對脫離體內一點產生順時針力矩的
對脫離體內一點產生順時針力矩的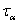 為正,反之為負。
為正,反之為負。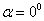 時,即橫截面上,
時,即橫截面上,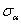 達到最大值,即
達到最大值,即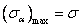 。當
。當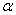 =
=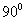 時,即縱截面上,
時,即縱截面上,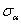 =
=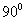 =0。
=0。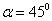 時,即與桿軸成
時,即與桿軸成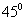 的斜截面上,
的斜截面上,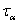 達到最大值,即
達到最大值,即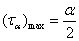
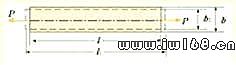
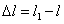 軸向線應變
軸向線應變 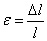 橫向變形
橫向變形 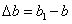
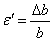 正負號規定 伸長為正,縮短為負。
正負號規定 伸長為正,縮短為負。 (3-5)
(3-5)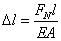 (3-6)
(3-6) ;
;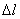 時,l長度內其N、E、A均應為常量。如桿件上各段不同,則應分段計算,求其代數和得總變形。即
時,l長度內其N、E、A均應為常量。如桿件上各段不同,則應分段計算,求其代數和得總變形。即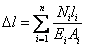 (3-7)
(3-7)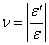 (3-8)
(3-8)
| 階 段 | 圖1-5中線段 | 特徵點 | 說 明 |
| 彈性階段 | oab | 比例極限  彈性極限 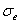 |  為應力與應變成正比的最高應力 為應力與應變成正比的最高應力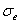 為不產生殘餘變形的最高應力 為不產生殘餘變形的最高應力 |
| 屈服階段 | bc | 屈服極限 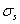 | 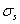 為應力變化不大而變形顯著增加時的最低應力 為應力變化不大而變形顯著增加時的最低應力 |
| 強化階段 | ce | 抗拉強度 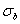 | 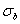 為材料在斷裂前所能承受的最大名義應力 為材料在斷裂前所能承受的最大名義應力 |
| 局部形變階段 | ef | | 產生頸縮現象到試件斷裂 |
| 性能 | 性能指標 | 說明 |
| 彈性性能 | 彈性模量E | 當 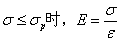 |
| 強度性能 | 屈服極限 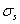 | 材料出現顯著的塑性變形 |
| 抗拉強度 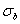 | 材料的最大承載能力 | |
| 塑性性能 | 延伸率 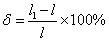 | 材料拉斷時的塑性變形程度 |
| 截面收縮率 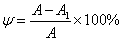 | 材料的塑性變形程度 |
 ]=
]=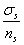 ; 脆性材料 [
; 脆性材料 [ ]=
]=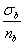
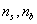 稱為安全係數,且大於1。
稱為安全係數,且大於1。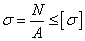 (3-9)
(3-9)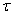 表示。
表示。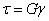 (3-10)
(3-10) 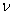 ),其數值由實驗決定。
),其數值由實驗決定。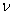 、G有下列關係
、G有下列關係 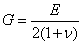 (3-11)
(3-11)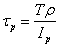 (3-12)
(3-12)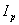 為該截面對圓心的極慣性矩,
為該截面對圓心的極慣性矩, 為欲求的點至圓心的距離。
為欲求的點至圓心的距離。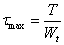 (3-13)
(3-13) 稱為扭轉截面係數,R為圓截面半徑。
稱為扭轉截面係數,R為圓截面半徑。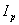 和扭轉截面係數
和扭轉截面係數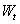 是截面幾何特徵量,計算公式見表3-3。在面積不變情況下,材料離散程度高,其值愈大;反映出軸抵抗扭轉破壞和變形的能力愈強。因此,設計空心軸比實心軸更為合理。
是截面幾何特徵量,計算公式見表3-3。在面積不變情況下,材料離散程度高,其值愈大;反映出軸抵抗扭轉破壞和變形的能力愈強。因此,設計空心軸比實心軸更為合理。
| 實心圓  (外徑為d) (外徑為d) | 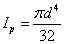 | |
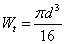 | ||
| 空心圓 (外徑為D, 內徑為d) | 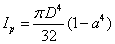 | 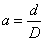 |
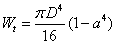 | ||
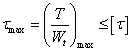 (3-14) 對等圓截面直桿
(3-14) 對等圓截面直桿 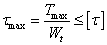 (3-15)式中
(3-15)式中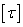 為材料的許用切應力。
為材料的許用切應力。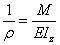 (3-16)
(3-16) 是變形後梁軸線的曲率半徑;E是材料的彈性模量;
是變形後梁軸線的曲率半徑;E是材料的彈性模量; 是橫截面對中性軸Z軸的慣性矩。
是橫截面對中性軸Z軸的慣性矩。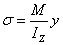 (3-17)
(3-17) 的意義同上;y是欲求正應力的點到中性軸的距離
的意義同上;y是欲求正應力的點到中性軸的距離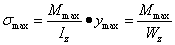 (3-18)
(3-18) 稱為抗彎截面係數。對於
稱為抗彎截面係數。對於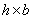 的矩形截面,
的矩形截面,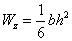 ;對於直徑為D的圓形截面,
;對於直徑為D的圓形截面, ;對於內外徑之比為
;對於內外徑之比為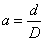 的環形截面,
的環形截面,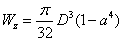 。
。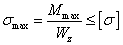 (3-19)
(3-19)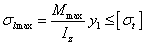 (3-20a)
(3-20a)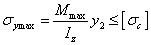 (3-20b)
(3-20b)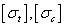 分別是材料的容許拉應力和容許壓應力;
分別是材料的容許拉應力和容許壓應力;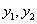 分別是最大拉應力點和最大壓應力點距中性軸的距離。
分別是最大拉應力點和最大壓應力點距中性軸的距離。 (3-21)
(3-21)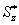 是距中性軸為y的橫線與外邊界所圍面積對中性軸的靜矩;
是距中性軸為y的橫線與外邊界所圍面積對中性軸的靜矩;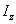 是整個橫截面對中性軸的慣性矩;b是距中性軸為y處的橫截面寬度。
是整個橫截面對中性軸的慣性矩;b是距中性軸為y處的橫截面寬度。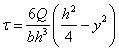 (3-22)
(3-22)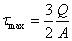 。
。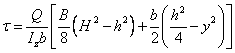 (3-23)
(3-23)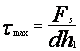 d為腹板寬度 h1為上下兩翼緣內側距
d為腹板寬度 h1為上下兩翼緣內側距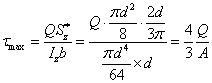 (3-25)
(3-25)
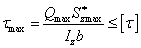 (3-26)
(3-26)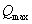 是樑上的最大切應力值;
是樑上的最大切應力值; 是中性軸一側面積對中性軸的靜矩;
是中性軸一側面積對中性軸的靜矩;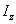 是橫截面對中性軸的慣性矩;b是
是橫截面對中性軸的慣性矩;b是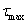 處截面的寬度。對於等寬度截面,
處截面的寬度。對於等寬度截面,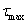 發生在中性軸上,對於寬度變化的截面,
發生在中性軸上,對於寬度變化的截面,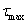 不一定發生在中性軸上。
不一定發生在中性軸上。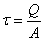 (3-27)
(3-27)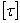 ,即
,即 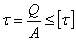 (3-28)
(3-28)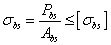 (3-29)
(3-29)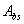 表示有效擠壓面積,即擠壓面面積在垂直於擠壓力作用線平面上的投影。當擠壓面為平面時為接觸面面積,當擠壓面為曲面時為設計承壓接觸面面積在擠壓力垂直面上的 投影面積。
表示有效擠壓面積,即擠壓面面積在垂直於擠壓力作用線平面上的投影。當擠壓面為平面時為接觸面面積,當擠壓面為曲面時為設計承壓接觸面面積在擠壓力垂直面上的 投影面積。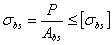 (3-30)
(3-30)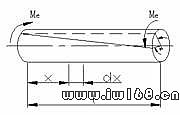
 (rad) (4.4)
(rad) (4.4)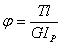 (rad) (4.5)
(rad) (4.5) 稱為圓軸的抗扭剛度。顯然,
稱為圓軸的抗扭剛度。顯然,
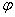 的正負號與扭矩正負號相同。
的正負號與扭矩正負號相同。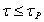 ;
;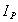 均為常量。當以上參數沿軸線分段變化時,則應分段計算扭轉角,然後求代數和得總扭轉角。即
均為常量。當以上參數沿軸線分段變化時,則應分段計算扭轉角,然後求代數和得總扭轉角。即 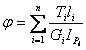 (rad) (4.6)
(rad) (4.6)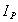 沿軸線連續變化時,用式(4.4)計算
沿軸線連續變化時,用式(4.4)計算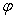 。
。 不得超過許可的單位長度扭轉角
不得超過許可的單位長度扭轉角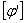 ,即
,即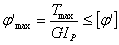 (rad/m) (4.7)
(rad/m) (4.7)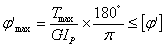 (
(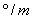 ) (4.8)
) (4.8)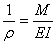

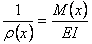
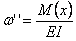 (4.9)
(4.9)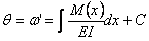 (4.10)
(4.10)
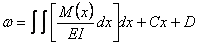 (4.11)
(4.11)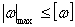 ,
,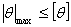 (4.12)
(4.12)
 ,可得
,可得 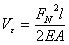 (4.14)
(4.14) 表示。線彈性範圍內,得
表示。線彈性範圍內,得 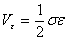 (4.15)
(4.15)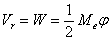
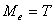 與
與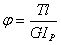 代入上式得
代入上式得 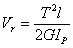 (4.16) 圖4.5
(4.16) 圖4.5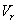 :
:  (4.17)
(4.17)
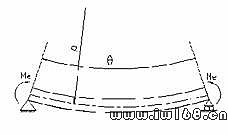
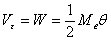
 與
與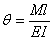 代入上式得
代入上式得 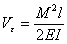 (4.18)
(4.18)  ,即
,即 (4.19)
(4.19)
| 靜 矩 | 慣性矩 | 慣性半徑 | 慣性積 | 極慣性矩 |
 | 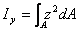 |  | 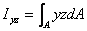 |  |
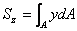 | 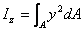 | 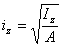 |
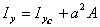
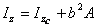
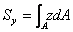 ,
,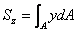 (Ⅰ-1)
(Ⅰ-1)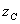 和
和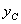 。則
。則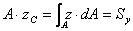
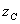 為
為 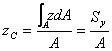

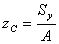 ,
, (Ⅰ-2)
(Ⅰ-2)
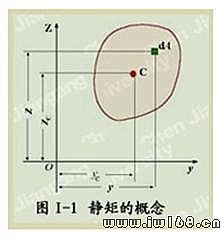
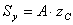 ,
,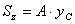
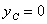 ,
,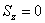 ;
;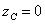 ,則
,則 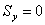 ;反之,若圖形對某一軸的靜矩等於零,則該軸必然通過圖形的形心。靜矩與所選坐標軸有關,其值可能為正,負或零。
;反之,若圖形對某一軸的靜矩等於零,則該軸必然通過圖形的形心。靜矩與所選坐標軸有關,其值可能為正,負或零。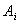 ,形心坐標為
,形心坐標為 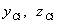 ,則其靜矩和形心坐標分別為
,則其靜矩和形心坐標分別為 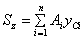 ,
,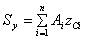 (Ⅰ-3)
(Ⅰ-3) ,
, (Ⅰ-4)
(Ⅰ-4)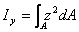 ,
, (Ⅰ-5)
(Ⅰ-5)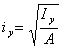 ,
,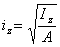 (Ⅰ-6)
(Ⅰ-6)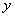 軸和對
軸和對 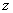 軸的慣性半徑。
軸的慣性半徑。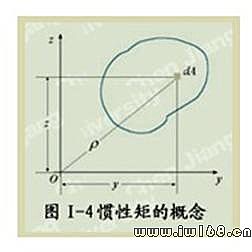
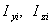 為分圖形的慣性矩,則總圖形對同一軸慣性矩為
為分圖形的慣性矩,則總圖形對同一軸慣性矩為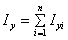 ,
, (Ⅰ-7)若以
(Ⅰ-7)若以 表示微面積
表示微面積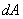 到坐標原點
到坐標原點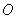 的距離,則定義圖形對坐標原點
的距離,則定義圖形對坐標原點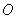 的極慣性矩
的極慣性矩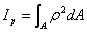 (Ⅰ-8)因為
(Ⅰ-8)因為 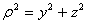
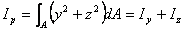 (Ⅰ-9)
(Ⅰ-9)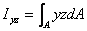 (Ⅰ-10)
(Ⅰ-10)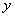 、
、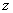 軸的慣性積。量綱是長度的四次方。
軸的慣性積。量綱是長度的四次方。 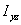 可能為正,為負或為零。若 y ,z 軸中有一根為對稱軸則其慣性積為零。
可能為正,為負或為零。若 y ,z 軸中有一根為對稱軸則其慣性積為零。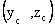 時,如圖Ⅰ-7所示,可得到如下平行移軸公式
時,如圖Ⅰ-7所示,可得到如下平行移軸公式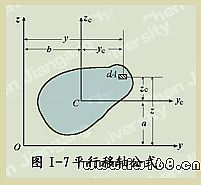
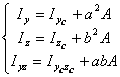 (Ⅰ-13)
(Ⅰ-13)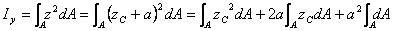
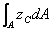 為圖形對形心軸
為圖形對形心軸 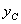 的靜矩,其值應等於零,則得
的靜矩,其值應等於零,則得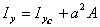
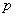 分解成與斜截面垂直的正應力
分解成與斜截面垂直的正應力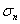 和相切的切應力
和相切的切應力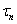 (圖13.1c),則其與主應力的關係為
(圖13.1c),則其與主應力的關係為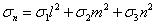
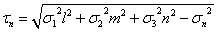 (13.2)
(13.2)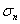 為橫坐標、
為橫坐標、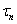 為縱坐標的坐標系中,由上式所確定的任意斜截面上的正應力
為縱坐標的坐標系中,由上式所確定的任意斜截面上的正應力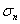 和切應力
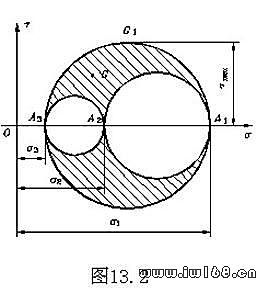
和切應力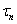 為由三個主應力所確定的三個圓所圍成區域(圖13.2中陰影)中的一點。由圖13.2顯見
為由三個主應力所確定的三個圓所圍成區域(圖13.2中陰影)中的一點。由圖13.2顯見