右圖為軸承工作時軸頸的位置。如圖所示，軸承和軸頸的連心線OO1與外載荷F（載荷作用在軸頸中心上）的方向形成一偏位角
。 軸承孔和軸頸分別用D和d表示，則軸承直徑間隙為：△=D-d
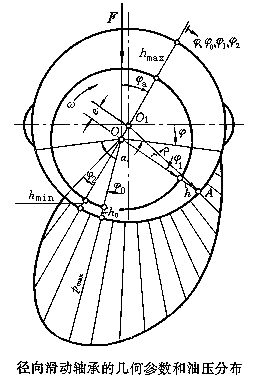
半徑間隙為軸承孔半徑R與軸頸半徑r之差，則
δ=R-r= Δ/2
直徑間隙與軸頸公稱直徑之比稱為相對間隙，以ψ表示，則
ψ=Δ/d= δ/r
軸頸在穩定運轉時，其中心O與軸承中心O1的距離，稱為偏心距，用e表示。偏心距與半徑間隙的比值，稱為偏心率，以χ表示，則
χ=e/δ
於是由圖可見，最小油膜厚度為
hmin=δ-e=δ(1-χ)=rψ(1-χ)
對於徑向滑動軸承，採用極坐標描述比較方便。取軸頸中心O為極點，連心線OO1為極軸，對應於任意角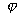
（包括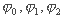
均由OO1算起）的油膜厚度為h,h的大小可在△AOO1中應用餘弦定理求得，即:
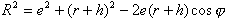
解上式得：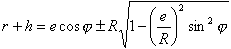
若略去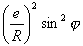
,並取正號,則得任意位置的油膜厚度為:
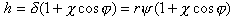
在壓力最大處的油膜厚度為：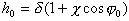 
式中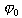
相應於最大壓力處的極角。
將雷諾方程寫成極坐標形式,即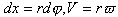
及h,h0 代入雷諾方程后得極坐標形式的雷諾方程
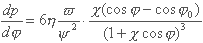
將上式從油膜起始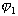角
到任意角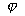
進行積分，得任意位置的壓力，即
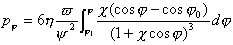
壓力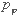
在外載荷方向上的分量為 ：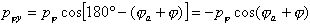 
把上式在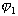到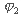
的區間內積分,就得出在軸承單位寬度上的油膜承載力,即
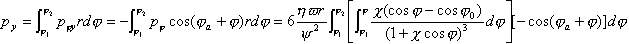
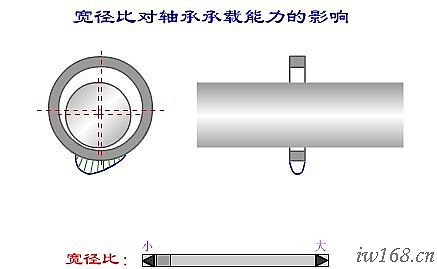
為了求出油膜的承載能力，理論上只需將py乘以軸承寬度B即可。但在實際軸承中，由於油可能從軸承的兩個端面流出，故必須考慮端泄的影響。這時，壓力沿軸承寬度的變化成拋物線分佈，而且其油膜壓力也比無限寬軸承的壓力低(左圖)，所以乘以係數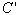
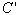，的值取決與寬度比B/d和偏心率
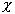的大小。這樣，在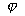角和距軸承中線為z處的油膜壓力的數學表達式為
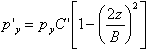
因此,對有限長軸承的總承載能力為
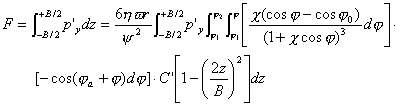
由上式得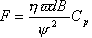
式中
於是得
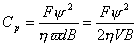
式中Cp為一個無量綱的量，稱為承載量係數，η為潤滑油在軸承平均工作溫度下的動力粘度，Pa·s；B為軸承寬度，m；F為外載荷，N；V為軸頸圓周速度，m/s。
Cp的積分非常困難，因而採用數值積分的方法進行計算，並作成相應的線圖或表格供設計應用。在給定邊界條件時，Cp是軸頸在軸承中位置的函數，其值取決於軸承的包角α(入油口和出油口所包軸頸的夾角)，相對偏心率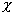
和寬徑比B/d。當軸承的包角α(α=120°，180°或360°）給定時，經過一系列的換算，Cp可表示為： 
若軸承是在非承載區內進行無壓力供油,且設液體動壓力是在軸頸與軸承襯的180度的弧內產生時，則不同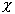
和B/d 的承載量係數Cp值見下表。
| B/d | | |||||||||||||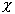
| 0.3 | 0.4 | 0.5 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.925 | 0.95 | 0.975 | 0.99 | |
| 承 載 量 系 數 Cp | ||||||||||||||
| 0.3 | 0.0522 | 0.0826 | 0.128 | 0.203 | 0.259 | 0.347 | 0.475 | 0.699 | 1.122 | 2.074 | 3.352 | 5.73 | 15.15 | 50.52 |
| 0.4 | 0.0893 | 0.141 | 0.216 | 0.339 | 0.431 | 0.573 | 0.776 | 1.079 | 1.775 | 3.195 | 5.055 | 8.393 | 21.00 | 65.26 |
| 0.5 | 0.133 | 0.209 | 0.317 | 0.493 | 0.622 | 0.819 | 1.098 | 1.572 | 2.428 | 4.261 | 6.615 | 10.706 | 25.62 | 75.86 |
| 0.6 | 0.182 | 0.238 | 0.427 | 0.655 | 0.819 | 1.070 | 1.418 | 2.001 | 3.036 | 5.214 | 7.956 | 12.64 | 29.17 | 83.21 |
| 0.7 | 0.234 | 0.361 | 0.538 | 0.816 | 1.014 | 1.312 | 1.720 | 2.399 | 3.580 | 6.029 | 9.072 | 14.14 | 31.88 | 88.90 |
| 0.8 | 0.287 | 0.439 | 0.647 | 0.972 | 1.199 | 1.538 | 1.965 | 2.754 | 4.053 | 6.721 | 9.992 | 15.37 | 33.99 | 92.89 |
| 0.9 | 0.339 | 0.515 | 0.754 | 1.118 | 1.371 | 1.745 | 2.248 | 3.067 | 4.459 | 7.294 | 10.753 | 16.37 | 35.66 | 96.35 |
| 1.0 | 0.391 | 0.589 | 0.853 | 1.253 | 1.528 | 1.929 | 2.469 | 3.372 | 4.808 | 7.772 | 11.38 | 17.18 | 37.00 | 98.95 |
| 1.1 | 0.440 | 0.658 | 0.947 | 1.377 | 1.669 | 2.097 | 2.664 | 3.580 | 5.106 | 8.186 | 11.91 | 17.86 | 38.12 | 101.15 |
| 1.2 | 0.487 | 0.723 | 1.033 | 1.489 | 1.796 | 2.247 | 2.838 | 3.787 | 5.364 | 8.533 | 12.35 | 18.43 | 39.04 | 102.90 |
| 1.3 | 0.529 | 0.784 | 1.111 | 1.590 | 1.912 | 2.379 | 2.990 | 3.968 | 5.586 | 8.831 | 12.73 | 18.91 | 39.81 | 104.42 |
| 1.5 | 0.610 | 0.891 | 1.248 | 1.763 | 2.099 | 2.600 | 3.242 | 4.266 | 5.947 | 9.304 | 13.34 | 19.68 | 41.07 | 106.84 |
| 2.0 | 0.763 | 1.091 | 1.483 | 2.070 | 2.446 | 2.981 | 3.671 | 4.778 | 6.545 | 10.091 | 14.34 | 20.97 | 43.11 | 110.79 |
