一、斜二等軸測投影的形成
斜二等軸測投影的投射方向S傾斜於軸測投影面P,這樣,軸測投影面P就不必與確定物體位置的三根直角坐標軸都傾斜相交,也可以得到物體的軸測投影。根據斜二等軸測投影的定義,如果使確定物體位置的一個坐標平面XOZ(既令坐標軸OZ處於鉛垂位置的正面)平行於軸測投影面P,則坐標平面XOZ上的兩根直角坐標軸OX、OZ也都平行於軸測投影面P,則軸測軸OX、OZ分別仍為水平、鉛直方向,且它們的軸向伸縮係數均為1,既p=r=1,這種斜二等軸測投影,稱為正面斜二等軸測投影,簡稱正面斜二測,如圖1a所所示。
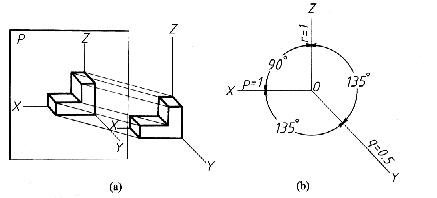
圖1 正面斜二等軸測的形成及其軸間角和軸向伸縮係數
二、正面斜二等軸測投影的投影特性
(1)正面斜二等軸測投影的投射方向S傾斜於軸測投影面P。(2)由於確定物體的一個坐標平面XOZ(或YOZ)平行於軸測投影面P,因此,物體與該坐標平面平行的平面圖形,其正面斜二等軸測投影反映真形,如圖1a所示。
三、正面斜二等軸測投影的軸間角和軸向伸縮係數
(一)軸間角由於確定物體位置的坐標平面之一的XOZ平行於軸測投影面P,所以,軸測軸OX和軸測軸OZ之間的軸間角反映真形(即∠XOZ=90°),變動投射方向S,可使軸測軸OY在軸間角∠XOZ的角平分線上,即∠XOY=∠YOZ=135°,如圖1b所示。(二)軸向伸縮係數同理,由於確定物體位置的平面之一的XOZ平行於軸測投影面P,因此,其上的兩根直角坐標軸OX、OZ也平行於軸測投影面P,它們的軸向伸縮係數相等,且為1(即p=r=1),變動投影方向,可使軸測軸OY的軸向伸縮係數為0.5(即q=0.5),如圖1b所示。
四、坐標平面(或其平行面)上圓的正面斜二等軸測投影的畫法圖2a為平行於坐標平面的圓的正面斜二等軸測投影。在坐標平面XOZ(或其平行面)上的圓的斜二等軸測投影反映該圓的真形;在坐標平面XOY和坐標平面YOZ上的圓的斜二等軸測投影是形狀、大小相同,方向不同的兩個橢圓,它們的長軸與圓所在的坐標平面上的一根軸測軸OX(或OZ)成7°10′(≈7°)的夾角。圖2~d示出了平行於坐標平面XOY的圓的斜二等軸測投影(橢圓)的畫法。
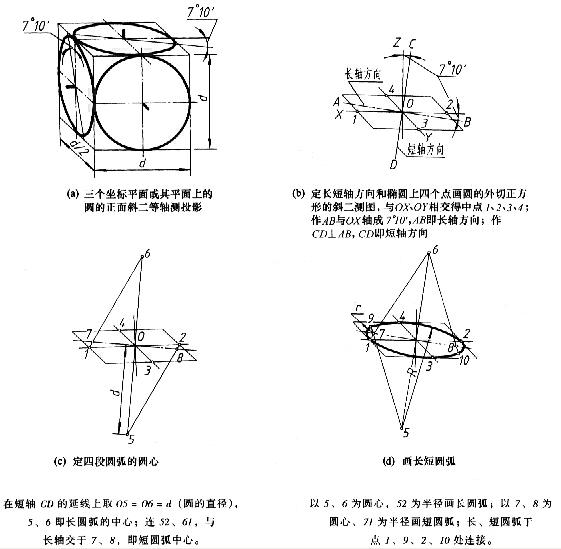
圖2 平行XOY平面上圓的斜二等軸測投影的畫法