工程上常見的曲面立體是迴轉體。迴轉體是由迴轉面或迴轉面與平面所圍成的立體。迴轉面是由母線(直線或曲線)繞某一 軸線旋轉而形成的。最常見的迴轉體有橢圓、圓錐、圓球和圓環。
畫迴轉體的投影圖時,一般應畫出各方向轉向輪廓的一個投影(其中與湖轉軸線的投影、對稱中心線重合的兩個投影,被省略不畫)和迴轉線的三個投影(其中兩個投影為直線、一個投影積聚成點,用對稱中心線表示,根據機械製圖規定表示軸線、對稱中心線均用細點畫線畫出,且要超出圖形的輪廓線3~5mm)。轉向輪廓線就是在某一投影方向上觀察曲面立體(如迴轉體)時可見與不可見部分的分界線。
迴轉體有一 重要特性,母線的任一位置稱為線素;母線上各點的運動軌跡皆為垂直於迴轉軸線的圓,這些圓周稱為緯線(緯圓,迴轉圓)。根據這一性質,可在迴轉面上作素線取點、線、稱為素線法;也可在迴轉面上作緯線取點、線,稱為緯線(緯圓,迴轉圓)法。
一、圓柱
圓柱是由圓柱面和頂圓平面、底圓平面圍成的。如圖4—5a所示,圓柱面可以看作是一條直母線AAσ繞與它平行的的軸線OO1旋轉而成.
(一)圓柱的投影
圖4—5b、c為軸線處於鉛垂線位置時的院住直觀圖及其投影圖。
1.投影分析
(1)圓柱的頂圓平面、底圓平面為水平面,其水平投影反映頂、底圓平面真形,且重合;正面投影和側面投影均積聚為平行於相應投影的直線a′b′c′d′、a’0c0’b0’d0’和d〃a〃c〃b〃、d〃0a〃0c〃0b〃0且等於頂、底圓的直徑。
(2)圓鏃面因其軸線為鉛垂線,故圓柱面上所有素線必須為鉛垂線,圓柱面為鉛垂面,其水平投影積聚為一圓,其與頂、底圓平面俯視輪廓的水平投影圓周相重合。沒一條素線的水平投影都積聚為點,且落在該圓周上。
(3)圖柱的正面投影應畫出該圓柱面正視轉向輪廓的正面投影。圓柱面上最左、最右兩條素線AA。和BB是正視方向可見部分(前半人圓柱面)和不可見部分(後半個圓柱面)的分界線,稱為正視轉視輪廓線。這兩條素線也可以表示了圓柱正面投影範圍,所以正視轉向輪廓線AA和BB的正面投影(矩形aabb中的aa和bb)必須畫出。而這兩條正視轉向輪廓線的水平投影積聚在圓周的最左點a(a')和最右點b(b');其側面投影a"a"T和b"b"現圓柱軸線的側面投影重合,省略不畫。
(4)圓柱面的側面投影應畫出該圓柱面側視轉向輪廓線的側面投影。圓柱面上最前、最後兩條素線CC0和DD0是側視方向可見部分(左半個圓柱面)和不可見部分(右半個圓柱面)的分界面,稱為側視轉向輪廓線。這兩條素線也表示了圓柱側面投影範圍,所以側視轉向輪廓線CC.和DD.的側面投影(矩形ddcc中的dd和cc)必須畫出。而這兩條正視轉向輪廓的水平投影積聚在圓周的最前點c(c)和最後點d(d);其正面投影c'c'和d'd '
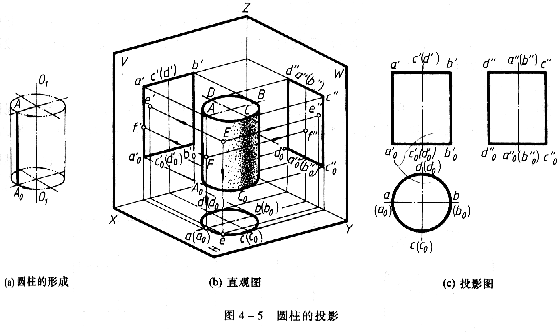
現圓柱軸線的正面投影重合,亦省略不畫。
2.作圖步驟
這裡應強調指出:圖示迴轉體時,必須畫出軸線和對稱中心線,均用細點畫表示。
畫軸線處於特殊位置時的圓柱三面投影圖時,一般先畫出軸線和對稱中心線(均用細點畫線表示);然後畫出圓柱面有積聚性的投影(為圓);再根據投影關係畫出圓柱的另外兩人個投影(為同樣大小的矩形),表明轉向輪廓線的投影。
(二) 柱表面上取點、線
軸線處於特殊位置的圓柱,其圓柱在軸線所垂直的投影面上的投影有積聚性,其頂、底圓平面的另兩個投影有積聚性。因此,在圓柱表面上取點、線,均可有積聚性作圖。對於圓柱表面上的點(如輪廓線上點)其投影均可直接作出,並表明可見性。
1.圓柱表面上取點
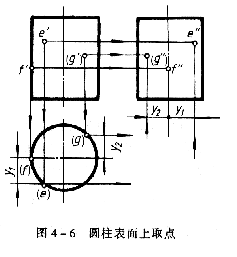
如圖4-6所示,已知圓柱面上點E、點和F和G的正面投影e'f'和(g'),試分別求出它們另兩個投影,其作法如下;
(1)求e'e"由於e'是可見的,所以點E在前半個圓柱面上,又因點E在左半個圓柱面上,所以e"也必為可見。作圖可利用圓柱面有積聚性的投影,先求出點E的水平投影(e)(在前半個圓周上),再由e'和?e?求出側南投影e"。
(2)求f、f"由於點F在圓柱的最左的正視轉向輪廓線上,姑另兩個投影均可直接求出。其水平投影(f)積聚在圓柱面水平投影(圓)的最左點上,即與最左正視轉向輪廓線的水平投影重合,其側面投影f"重合在圓柱軸線的側面投影上,且f"可見。
(3)求g、g"由於(g')為不可見,所以點G在後半個圓柱面上,又因點G在右半個圓柱面上,所以(g")也為不可見。作圖時可利用圓柱有積聚性的投影,先求出點G的水平投影(g)(在後半個圓周上),再由(g')和(g)求出側面投影(g")。
2.圓柱表面上取線
在圓柱表面上取線,可先取屬於線上的特殊點,再取屬於線上一些一般點,經判別可見性后,再順次連成所要取的線。如圖4—7所示,以知圓柱表面素線上的直線AB的正面投影a'b'和一段平行於水平面的迴轉圓弧BC的正面投影b'c'(積聚成直線),試求其另兩個投影,其作法如下:
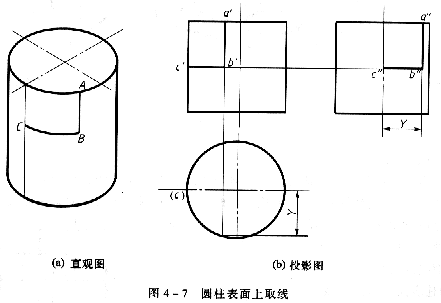
(1)求ab、a"b"由於直線AB在圓柱表面素線上(AB平行於軸線),利用圓柱面水平投影的積聚性,即可求出直線AB的水平投影a(b)(積聚在圓周)上,再按投影投影關係求出a"b"。由於直線AB 在左半個圓柱面上,其側面投影a"b"為可見。
(2)求bc、b"c"由於圓柱表面上的一段迴轉圓弧BC平行於水平面,姑水平投影bc反映真形——積聚在圓柱投影的圓周上),再按投影關係求出b"c"(積聚成直線)。BC在左半個圓柱面上,其側面投影b"c"為可見。
二、圓錐
圓錐是有圓錐面和底圓平面圍成的。如圖4—8a所示,圓錐面何以看作是一條直母線SA繞與它相交的軸線○○1迴轉而形成。在圓錐面上任一位置的素線,均交於錐頂S。
(一)圓錐的投影
圖4一8b、c為軸線處於鉛垂線位置時的圓錐直觀圖及其投影圖。
1.投影分析
(1)底圓平面為水平面,其水平投影為圓,且反映底圓平面的真形。底圓平面的正面投影和側面投影均積聚為直線,且等於底圓的直徑。
(2)圓錐面的三個投影均無積聚性。圓錐面的水平投影為圓,且與圓錐底圓平面的水平投影重合,整個圓錐面的水平投影都可見。
(3)圓錐面的正面投影,要畫出該圓錐面正視轉向輪廓線的正面投影。圓錐面上最左,最右兩條素線SA、SB的正面投影s'a'、s'b',也是圓錐面的正視轉向輪廓線的正面投影,正視轉向輪廓線是圓錐面在正面投影中(前半個圓錐面)可見和(後半個圓錐面)不可見的分界線。它們還表示了圓錐面的投影範圍,而這兩條正視轉向輪廓線SA、SB的水平投影sa、sb與圓錐水平投影(圓)的水平對稱中心線重合,省略不畫;其側面投影s"a"、s"b"與圓錐軸線的側面投影重合,也省略不畫。
(4)圓錐面的側面投影,要畫出該圓錐面測視轉向輪廓線側面投影。圓錐面上最前、最後兩條素線SC、SD的側面,也是圓錐面的側視轉向輪廓線的側面投影,側視轉向輪廓線是圓錐面投影中(左半個圓錐面)可見和(右半個圓錐面)不可見的分界線,它們還表示了圓錐面的投影範圍。而這兩條側視轉向輪廓線SCSD的正面投影與圓錐軸線的正面投影重合,省略不畫;其水平投影與圓錐水平投影(圓)的垂直對稱中心線重合,也省略不畫。
2.作圖步驟
畫軸線處於特殊位置時的圓錐三面投影圖時,一般先畫出軸線和對稱中心(用細點畫線表示);然後畫出圓錐反映為圓的投影;再根據投影管轄化出圓錐的另兩個投影(為同樣大小的等腰三角形)。
(二) 面上取點、線
軸線處於特殊位置的圓錐,只有底面兩個投影有積聚性,而圓錐面的三個投影都沒有積聚性。因此,在圓錐表面上取點、線,除處於圓錐面轉向輪廓線上特殊位置的點或底圓平面的點,可以直接求出之外而其於處於圓錐表面上一般位置的點,則必須用輔助線(素線法或緯線法)作圖,並表明可見性。
1.圓錐表面上取點
如圖4一9所示,以知圓錐表面上E和F的正面投影e'和f',試求它們的兩個投影,其作法如下:
(1)求e、e"由於點E為圓錐面上右前方的一般為點,故需用輔助線作圖。
①素線法 由於過錐頂的圓錐面上的任何素線均為直線,故可過E及錐頂S作錐面的素線SI。即先過e'作s'l',由l'求出l和l,連接sl和s"l",分別為輔助線SI的水平投影和側面投影。則E的水平投影和側面投影必在SI的同面投影上,從而即可求出e和(e")。e可見,又應E在由半個錐面上,所以(e")為不可見.
② 線(緯圓、迴轉圓)法 過E在圓錐面上作一水平輔助圓(緯圓),點E的投影
在該緯圓的同面投影上。即先過e'作水平線2'3',它是緯圓的正面投影,2'3'的長度即為該緯圓的直徑,從而可畫出圓心與s重合的該緯圓的水平投影;由e'作投影連線,與緯圓的水平投影(圓)交於點e,再由e'和e求出(e")
(2).求f、f"由於點F在最左正視轉向輪廓線SA上,為圓錐面上特殊位置的點,故可直接求出f和f"。由於f'在s'a'上,則f必在sa上,f"必在s"a"上。且f、f"均為可見。
2.圓錐表面上取線
在圓錐表面上取線,可先取屬於線上的特殊點,再取屬於線上的一些一般點,經判別可見性后,再順次連成所要取的線。如圖4一10所示,以知圓錐表面素線上的直線AB的正面投影a'b'和圓錐表面少年宮垂直於軸線(圓錐軸線垂直於水平面)的一段迴轉弧CD的正面投影c'd'(積聚成直線)。試求另兩個投影,作法如下:
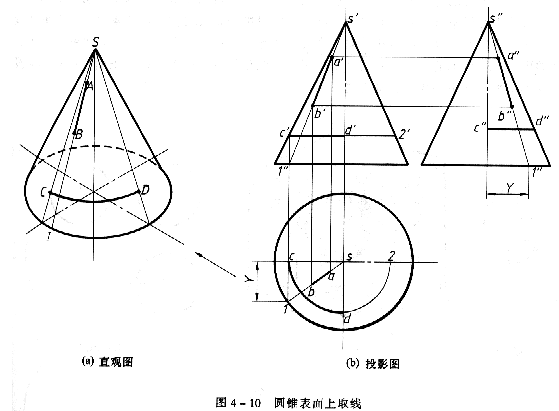
(1) 求ab、a"b"由於直線AB在圓錐表面素線上,故餓過直線AB作錐面上的素線SI。即先過a'b'作s'l',由l'先求出l,再求出l",連接s、l和s"、l",分別為輔助線SI的水平投影和側面投影。則直線AB的水平投影和側面投影必SI的同面投影上,從而即可求出ab和a"b"。Ab可見;因直線AB在左半個圓錐面上,所以a"b"也可見。
(2)求圓錐表面上一段迴轉圓弧CD的水平投影和側面投影 由於圓錐表面上垂直於軸線(軸線垂直水平面)的一段迴轉圓弧CD必平行於水平面,故水平面投影反映真形。過c'd'作c'2'(迴轉圓直徑),由c'2'求出c2,即可求出cd。其側面投影和正面投影同樣積聚成直線,由於CD在鄒半個圓錐面上,故c"d"亦為可見。
三 圓球
如圖4一11所示,圓球面可以看作由一圓為母線,繞其通過圓心且在同一平面的軸線(直徑)迴轉而形成的曲面。
由於過球心(圓心)可作無數條軸線(直徑),故任一平面與圓球的交線皆為一圓周。由於圓球面為光滑曲面,故圖示圓球面時只需畫出迴轉軸線、對稱中心及轉向輪廓線即可。 (一)圓球的投影
圖4一 11b、c為圓球直觀圖及其投影圖。
1.投影分析
圓球的三面投影均為等直徑的圓,它們的直徑為球的直徑。
(1)正面投影的圓是圓球正視轉向輪廓線(過球心平行於正面的轉向輪廓線,是前、後半泅面的可見與不可秒年的分界線)的正面投影。而圓球正視轉向輪廓線的水品投影與圓球水平投影的水平對稱中心線重合;其側面投影與圓球側面投影的垂直對稱中心重合,都省略不畫。
(2)水平投影的圓是圓球俯視轉向輪廓線(過球心平行於水平面的轉向輪廓線,是上、下半球面的可見與不可見的分界線)的水平投影。而圓球俯視轉向輪廓線的正面投影和側面投影均分別在其水平對稱中心線上,都省略不畫。
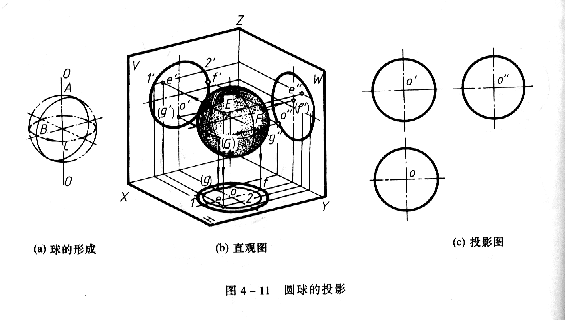
(3)側面投影的圓是圓球側視轉向輪廓線(過球心平行於側面的轉向輪廓線,是左、右半球的可見於不可見的分界線)的側面投影。而圓球側視鑽鄉輪廓線的正面投影和水平投影均分別在其垂直對稱中心線上,都省略不畫。
2.作圖步驟
畫圓球的三面投影時,可先畫出確定球心0的三個投影0、0'、0"、位置的三個對稱中心線;再以球心的0三個投影0、0'、0"為圓心分別畫出三個現圓球直徑相等的圓。
(二). 圓球表面上取點、線
由於圓球的三個投影均無積聚性,所以在圓球表面上取點、線、除屬於轉向輪廓上的特殊點可直接求出之外,其餘處一般位置的點,都需要作輔助線(緯線)作圖,並表明可見性。
1.圓球表面取點
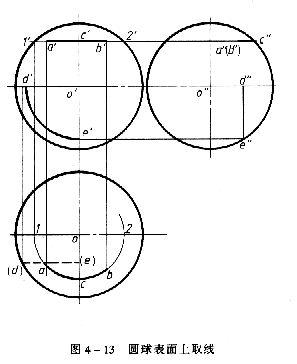
如圖4-12所示範區,已知圓面球表面上點E、F、G的正面投影e、f'、(g'),試求出另兩個投影,其作法如下:
(1)求e、e' 由於e'是可見的,且為前半個圓球面上的一般位置點,故可作緯圓(正平圓、水平圓或側平圓)求解。如過e'作水平線(緯圓)與圓球正面投影(圓)交於1'、2',以1'2'為直徑在水平投影上作水平圓,則點E的水平投影Ent 在該緯圓的水平投影上,再由e、e"求出e"。因點E位於上半個圓球面上,故e為可見,又因為E在左半個圓球面上,故e"也為可見。
(2)求f、f"和g、g"由於點F、G是圓球面上特殊位置的點,故可直接作圖求出。由於f"可見,且在圓球正轉向輪廓線的正面投影(圓)(上,故水平投影f在水平對稱中心線上,側面投影(f")在垂直中心對稱線上。因點F在上半球面上,故F為可見,又因點在右半個球面上,(f")為不可見。由於(g')為不可見,且在垂直對稱中心線上,故點G在後半個球面的側視轉向輪廓線上,可由(g')先求出g",為可見;再求出(g),為不可見。
2.圓球表面上取線
在圓球表面上取線,可行求出屬於線上的一系列點(特殊點、一般點),判別可見性,再順次連成所要取的線。
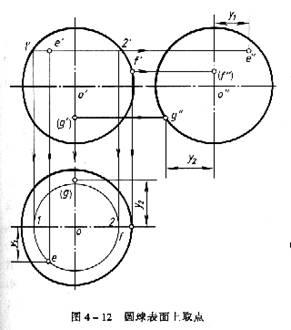
如圖4-13所示,已知圓球表面上平行水平面的一段迴轉圓弧ACB的正面投影a'c'b'和平行正面的一段迴轉圓弧DE的側面投影de,試分別求另兩個投影,作法如下:
(1)求acb、a"c"b"由於a'c'b'是可見的,且平行於水平面,故可作緯圓(水平圓)求解。過a'c'b'作水平面與圓球正面(圓)交點1'2',以1'2'為直徑在水平投影上作水平圓,則水平圓弧ACB的水平投影acb必在該緯圓上,再由a'c'b'、acb求出a"c"b"。因水平圓弧ACB位於上半個圓球面上,故acb為可見。又因水平圓弧ACB中CB部分位於右半個圓球面上,側面投影為不可見,故在本圖中的側面投影c"(b")與可見的AC側面投影a"c" 重影
(2)求d'e'、de由於d"e"是可見,且平行於正面,故可用緯圓(正平圓)求解。以側面投影d"e"半徑,在正面投影上作正平圓的正面投影,即得DE的正面投影d'e'(1/4緯圓),再由d"e"、d'e'求出de。因正平圓弧DE位於前半個圓球面上,故d'e'為可見。又因為平圓弧DE位於下半個圓球面上,故(d)(e)為不可見(畫成虛線)
四、圓環
如圖4-14所示,圓環可以看作是由一圓為母線,繞與其共面但不通過圓心的軸線迴轉而形成。其中,外半圓BAD迴轉形成外圓環面,內半圓BCD迴轉形成內環面。
(一)環的投影
圖4-14所示,b、c為軸線處於圓軸線位置時的圓環直觀圖及其投影圖。
1.投影分析
圓環的正面投影和側面投影形狀完全一樣;水平投影是三個同心圓(其中有一細點畫線圓)。
(1)水平投影的三個同心圓 其中的細點畫線圓是母線圓心軌跡的水平投影,也是內外環面上的上、下兩個分界圓的水平投影重合;內外粗實線圓是圓環面上最小、最大緯線圓的水平投影,也是內、外圓環面俯視轉向輪廓線(內外圓環的可見部分與不可見部分的分界線)的水平投影。
(2)正面投影上的兩個小圓(一半粗實線,一半虛線)是外、內圓環面正視轉向輪廓線上最左、最右兩和素線的正面投影。其中,虛線半圓是內環面上正視轉向輪廓線的正面投影,也是內環面上前半環面與後半環面的分界線的正面投影,前、后內環面的正面投影均不可見,故畫成虛線。粗實線半圓是外環面上正視轉向輪廓線的正面投影,也是外環面上前半環面與後半環面、可見和不可見的分界線的正面投影。
正面投影上、下兩條與小圓相切的橫向直線是圓環面上最高,、最低兩條緯線圓的正面投影的積聚;也是內、外環面上、下兩個分界的正面投影的積聚。
(3)側面投影上的兩個小圓(一半粗實線、一半虛線)是外、內圓環面側視轉向輪廓線上最前、最後兩條素線的側面投影。其中,粗實線半圓是外環面上側視轉向輪廓線的側面投影,也是外環面上左半環面與右半環面、可見和不可見的分界線的側面投影;虛線半圓是內環面上側視轉向輪廓線的側面投影,也是內環面上左半環面與右半環面的分界線的側面投影,左右內環面的側面投影均不可見。
側面投影上、下兩條與小圓相切的橫向的直線是圓環上最高、最低兩條緯線圓的側面投影,也是內外環同上、下兩個分界的側面投影的積聚。
2.作圖步聚
畫圓環三面投影圖時,應畫出圓環面的迴轉軸線、對稱中心線(均用細點畫線表示)及內、外環面的轉向輪廓線。
一般先畫出圓環軸線 及對稱中心線,再畫圓環在軸線所垂直的投影面上的投影(三個同心圓);然後畫另兩個形狀相同的投影。
(二)環表面上取點
在圓環表面上取點,需用緯線(緯圓)作圖求解。如圖4一 14c所示,已知圓環面上點E、F的正面投影e'、(f'),試求其另兩個投影,其作法如下:
(1)求e'、e"由於e'是可見的,且E位於上半個外環面上。故e為可見。又因E在左半個外環面上,故e"也為可見的。先過E點作一平行於水平投影面的水平緯圓,該緯圓在正面投影上為過e'的直線1'2',則它的水平投影為一 直徑等於線段1'2'的緯圓,e必在此圓周上,故由e'可求出e,在由e'、e可求出e"(唯一解)。
(2)求f、f"由於(f')不可見,則過點F可作內外環面上的兩條緯線,即點F必在內環面(前或后)或後半個外環面上,故共有三個解。所以點F的歲平投影可為f1或f2或f3(因為F在上半個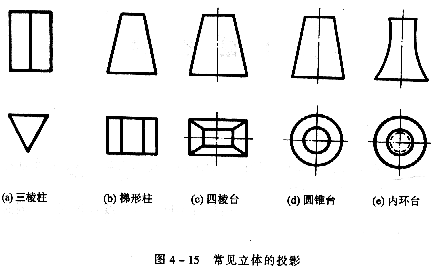
圓環上,故為可見);側面投影可為(f"1)或(f"2)或(f"3)(因為點F在右半個圓環上,故為不可見)。
在上述兩類立體中,還有一些常見的立體,其投影如圖4一 15所示。