第二節 正軸測投影圖
一.正等測圖的形成
現以正立方體為例來說明正等測圖的形成過程,如圖9-3所示:
1.把正立方體放置在水平面上,並使正立方體的前面平行於正面(軸測投影面)。當投影光線垂直正面投射時,正立方體的投影是個正方形(圖9一3a)。它只能反映正立方體一個面的形狀,因而沒有立體感。
2.如果將正立方體從圖9一3a所示的位置,按箭頭所指的方向繞一鉛垂軸旋轉45°后,再進行投影,所得正立方體的投影是兩個相連的長方形(圖9一3b)。因為它只反映了正立方體兩個面的形狀,所以立體感也不強。
3.如果再把正立方體從圖9一3b所示的位置繞一側垂軸向前旋轉,使它的對角線OA垂直於正面(圖9一3c),則正立方體的前面、側面和頂面都與軸測投影面傾斜相同的角度。此時,正立方體在軸測投影面上的投影就呈現三個相連的菱形。因為在一個投影面中同時反映出正立方體互相垂直的三個面的形狀,所以投影就具有較好的立體感,這就是正立方體的正等測圖。
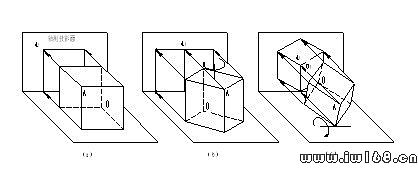
圖9-3 正等測圖的形成
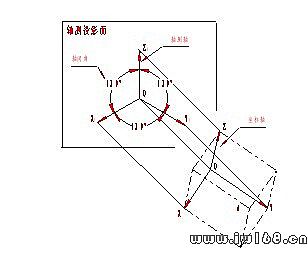
圖9-4 正等測的軸測軸和軸間角
為了更清楚地說明正等測圖的形成和特點,我們把正立方體上的0點作為直角坐標系的原點(圖9一4),並假設過0點的三個棱邊為X、Y、Z三個坐標軸。這三個坐標軸必與正立方體的對角線OA構成相等的角度。當OA垂直於軸測投影面時,則X、Y、Z與軸測投影面傾斜的角度都相等。因此,只要物體上三個互相垂直的坐標軸與軸測投影面傾斜相同的角度,就可得到正等測圖。
二、正等測圖的投影特性
正等測圖實際上也是正投影圖。因此,它具有正投影的一般性質,如直線的投影一般仍為直線,平行直線的投影仍互相平行等。但是,要正確地繪製正等測圖,還須了解它的另外三個特性:
1.物體上的三個坐標軸的軸測投影叫做軸測軸,在正等測投影中,由於三個坐標軸OX、OY和OZ與軸測投影面傾斜相同的角度(約為35o),所以它們的軸測投影O1X1、O1Y1、O1Z1就一定按相同的比例縮短,縮短后的長度與原長的比值(即O1X1/OX、O1Y1/OY、O1Z1/OZ),叫軸向縮短係數,約為0.82。物體上凡與坐標軸平行的直線,其軸測投影也必與相應的軸測軸平行,長度均應縮短為原長的0.82倍。
2. 在軸測圖上軸測軸之間的夾角(∠X1O1Z1、∠X1O1Y1、∠Y1O1Z1)叫做軸間角(圖9-4)。在正等測圖中三個軸間角相等,都是120o,畫圖時須先畫出。
3.物體上凡不平行於軸測投影面的平面,其軸測圖都變形,例如,正多邊形變成了斜多邊行,圓變成了橢圓。
三、正等測圖的基本畫法
根據上述正等測投影的特性,可以畫出長方塊的正等測圖,如圖9-5所示。
為作圖簡便,常把正等測圖的軸向縮短係數簡化為1,也就是零件上凡是平行於坐標軸的直線,在軸測圖上都按實際尺寸畫出,不在縮短。圖9-6所示的軸測圖就是按簡化的縮短係數畫出的。它比用縮短係數0.82畫出的軸測圖放大了1.22倍。
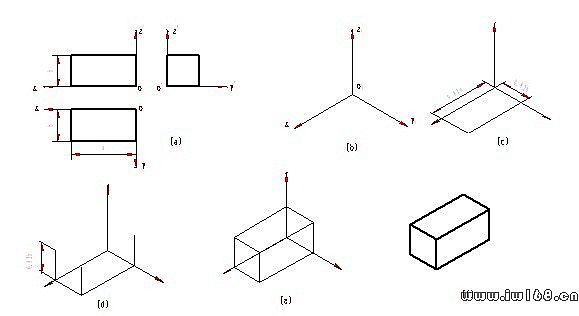
圖9-5 長方體正等測圖的畫圖步驟
(a)定坐標軸 (b)作軸測軸 (c)取長方體長度、寬度的0.82倍畫出長方體的底面 (d)從底面四個頂點畫平行z1軸的四條稜線,取其高度的0.82倍 (e)連起長方體的頂面 (f)描深看得見的輪廓線
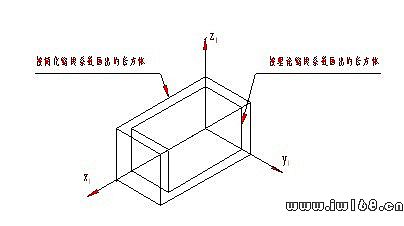
圖9-6 按簡化係數畫圖
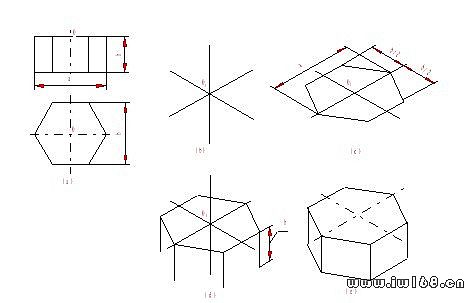
圖9-7 正六稜柱的正等測圖的畫法
通過上述兩個形體的正等測圖的畫圖過程看出,畫軸測圖時,先在物體視圖上選定適當的坐標原點及坐標軸,並在圖紙上畫出相應的軸測軸,然後把物體上的某些點,根據視圖中給出的坐標,確定它們在軸測坐標系中的位置,進而畫出物體上某些線和面,並逐步完成全圖。這種畫法叫做坐標定點法,是繪製軸測圖的一種基本方法。下面所舉的幾個例題都是按照這種方法畫出來的。
四.圓的正等測圖
多數物體上都有圓和圓弧形結構,而這些圓多數又平行於某兩個坐標軸所決定的坐標面。這裡主要介紹平行於各坐標面的圓在軸測圖上的畫法。
假設在正立方體的三個面上,各有一個直徑為d的內切圓如圖9-8所示。這三個圓都與軸測投影面傾斜相同的角度,因此各圓的正等測投影均為形狀相同的橢圓,並且也都內切於三個相同的菱形。根據它們的幾何關係,可以推斷出各橢圓在軸測投影中的三個特點:

圖9-8 圓的正等測投影
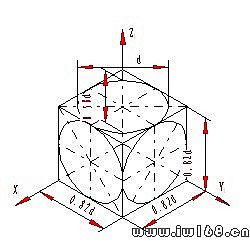
圖9-9 橢圓的長、短軸的方向
1.橢圓長、短軸的方向(圖9-9)
平行於X1-Y1面的橢圓,其長軸垂直於Z1軸;平行於X1-Z1面的橢圓,其長軸垂直於Y1軸;平行於Z1-Y1面的橢圓,其長軸垂直於X1軸。橢圓的長軸與短軸垂直。
2.橢圓長、短軸的大小
橢圓長軸是圓上平行於軸測投影面的那條直徑的投影(見圖9-8中11 2 2),長度就等於圓的直徑d。經幾何計算,橢圓短軸的長度等於0 .58d。
3.一對共軛直徑
在正立方體各個面上的圓中分別平行於兩個坐標軸的一對直徑稱為共軛直徑,在軸測投影圖中仍平行於軸測投影軸,其長度為0.82d(如圖9-8中的a1b1、c1d1)。在軸測圖上,常以這兩條直徑作為畫橢圓的定位線。畫橢圓時,先把它們畫出。採用簡化縮短係數畫橢圓時,上述數據均擴大到1.22倍(圖9-10)。

圖9-10 圖增大1.22倍
知道了橢圓長、短軸的方向和大小,就可以按圖9-10的方法畫出橢圓。但這種畫法比較麻煩,一般常用“四心法”近似地畫橢圓。具體作圖方法見圖9-11。其中圖9-11a 過O點作軸測軸AB、CD、EF,作水平線與AB垂直,就是橢圓長軸方向,以O為圓心,以d為直徑畫一個圓。圖9-11b分別以A、B為圓心,AD或BC為半徑畫兩個大弧,與AB相交於H和G。圖9-11c以O為圓心,OG為半徑,作弧與橢圓長軸交於I和II。圖9-11d連圖IB,並延長交大圓弧於K(兩圓弧切點)。以I、II兩點為圓心,IK為半徑,作弧把兩個大圓弧連接起來。
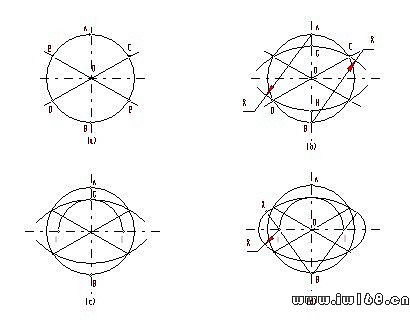
圖9-11 正等測圖中橢圓的近似畫法
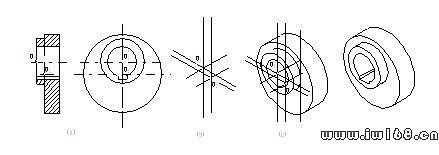
圖9-12 凸輪的正等測圖的畫法
9-12示出了用“四心法”繪製凸輪的正等測圖。其中圖9-12a定出坐標軸。圖9-12b過各圓心畫出軸測軸。圖9-12c由前向後畫出各圖。圖9-12d描深可見輪廓線。
五.圓柱、圓錐、圓球及圓環的正等測圖
物體上經常遇到柱、錐、球、環等基本體,它們的軸測投影圖的畫法及要點如表9-1所示。圖中各例都按簡化縮短係數畫出。
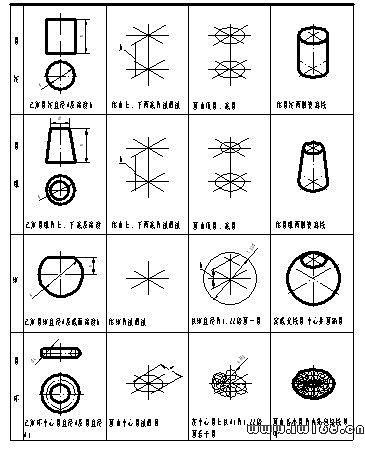
表9-1 基本幾何體正等測圖的畫法
六.物體上平板圓角的畫法
物體底板、凸台、凸緣部分的轉角處,常做成圓角,如圖9-13a所示。在軸測圖上,圓角可按圖9-13b所示的方法繪製,R弧在軸測圖上均為橢圓的一段,左邊圓角可用大圓弧r1畫;右邊圓角可用小圓弧r2畫,其中圖9-13c是簡便畫法。在平板的圓角上各量R值得切點,並自該點作各邊的垂直線,它們相交得A、B兩點,A、B兩點就是r1、 r2的圓心,垂直線長度就是、r1或 r2。
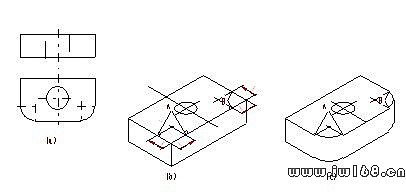
圖9-13 平板圓角軸測圖的畫法
七.正等測圖畫法綜合示例
[例1] 根據視圖畫出切割體的正等測圖如圖9—14所示。
由於彎管各節圓柱斜口的傾角相同,如果把各節圓柱一反一正疊置在一起,恰好構成一完整的圓柱管[圖8-11(a)],其展開圖為一矩形。因此可以先畫出首節(或尾節)的展開圖,再以它為樣板,畫出其餘幾節的展開圖[圖8-10(b)和圖8-11(b)]。這樣可使畫圖簡單、排料合理、下料方便(注意每節圓柱要留有切割余量)。
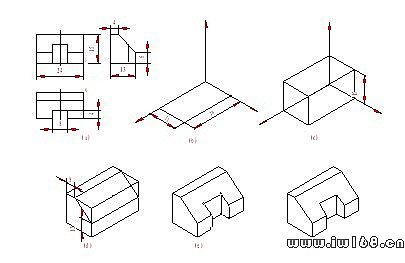
圖9-14 切割體正等測圖的畫法
(a)定坐標位置 (b)畫軸測軸及長方體的底面 (c)畫出長方體 (d)切去前上傾斜部分 (e)畫出前中央凹槽 (f)描深
[例2] 根據視圖畫出支架的正等測圖如圖9—15所示。 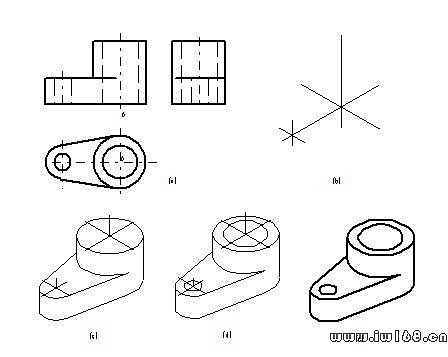
圖9-15組合體正等測圖的畫法
(a)定坐標圓點 (b)畫坐標軸 (c)畫底板和圓柱 (d)畫圓孔 (e)描深