第十章 透視圖
第一節 透視圖的基本概念
一.透視投影
透視投影必須具備三個條件,即物體、投影面和點光源。將投影面置於物體與點光源之間,而後使物體向向投影面進行投影的過程,稱為透視投影。
圖10-1表示了透視投影的基本原理。人的眼睛透過玻璃(畫面)觀察建築物模型,則無數條視線與玻璃面相交而形成的圖形即為透視投影。透視的原意就是透過畫面觀察(視)物體而畫出的圖形。因此透視圖相當於以人的一隻眼睛為投影中心進行投影所得的圖樣,所以說,中心投影的原理是畫透視圖的理論依據。
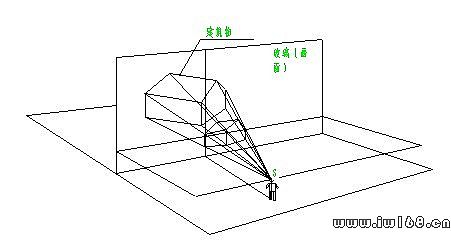
圖10-1 透視原理
二、基本術語
為了下面敘述的方便,先讓我們通過圖10-2了解透視圖的一些基本術語。
1. 基面H—放置物體的水平面或地平面。常選取三面正投影體系中的水平面H作基面。
2. 畫面P—透視圖所在的平面。本篇規定畫面與基面垂直。
3. 基線OX&mdasah;畫面P與基面H的交線。
4. 視點S—即投影中心,相當於觀察者眼睛所在的位置。
5. 站點S—視點S在基面上的正投影,相當於觀察者站立的位置。
6. 主視線Ss′—通過視點與畫面垂直的一條視線,也稱視軸。
7. 心點s′—主視線與畫面的交點。
8. 視平面—過視點的水平面,全部水平視線都在視平面上。
9. 視平線hh—視平面與畫面的交線。
10.視高—視點到基面的距離。
11.視距—視點到畫面的距離。
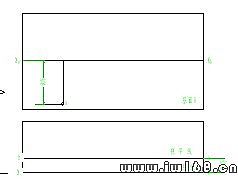
在作圖時,要把基面H和畫面P沿著基線OX拆開攤平,將畫面P保持不動,基面H放在畫面P的正下方或正上方(如同三面正投影中,正面投影於水平投影長對正的關係),見圖10-3。拆開后,因基線OX是畫面與基面的交線,故將畫面上的基線仍用OX表示,而將基面上的基線看作畫面P在基面上的正投影,用OhXh表示。基面和畫面的邊框一般省略不畫。
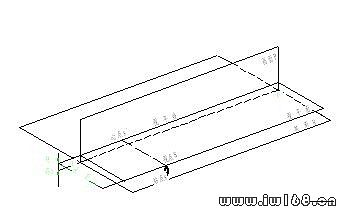
圖 10-2 基本術語
(a)正等測 (b)正二測 (c)斜二測
三、直線的滅點
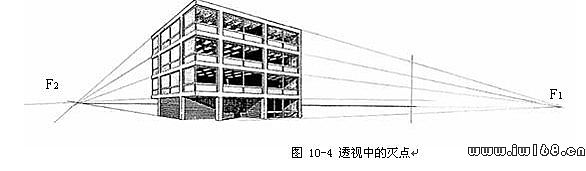
在圖10-4中,平行於房屋長度方向的相互平行的直線,離畫面逾遠逾靠攏,直至相交於一點F1,稱F1為該直線的透視滅點。同樣,平行於房屋寬度方向的平行線延長後會相交於另一個滅點F2。一般情況下,直線的透視都應該具有滅點,這是透視圖的重要特點。本章第三節中將介紹直線滅點的確切定義。
四、透視圖的分類
1.一點透視
物體的長寬高三個方向中,若只有一個方向的直線在透視圖中具有滅點則稱為一點透視。見圖10-5,房間內平行於寬度方向的水平線相交於滅點F,長度與高度方向與畫面平行,因而這兩個方向的直線在透視圖中均沒有滅點,所以稱一點透視。
2.兩點透視
在圖10-4中,建築物的長度方向與寬度方向均與畫面傾斜,除了高度方向的直線平行於畫面,在透視圖中仍相互平行,即沒有滅點外,長度和寬度兩個方向的直線在透視圖中分別消失在F1和F2兩個滅點,故稱為兩點透視。由於物體與畫面成一定角度,故又稱為成角透視。
3.三點透視
當物體的長、寬、高三個方向均與畫面傾斜時,則三個方向的直線在透視圖中都有滅點,這就是三點透視,見圖10-6。這種透視多用來表現高達雄偉的建築物,在一般工程繪畫中,有時也用它來跨大建築物的造型。當人們位於近處仰視高大的物體時,所看到的物體形象即為三點透視圖。
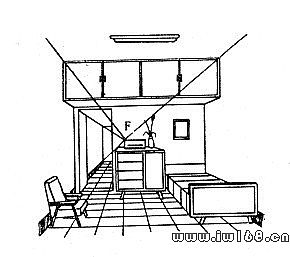
圖10-5 一點透視
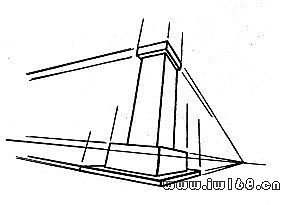
圖10-6 三點透視