3.2 點、直線和平面的投影分析
3.2.1 點的投影
一、三投影面體系
由正立投影面V、水平投影面H 和側立投影面W 三個互相垂直的投影面構成的投影面體系稱為三投影面體系。正立投影面簡稱正面或V 面、水平投影面簡稱水平面或H 面、側立投影面簡稱側面或W 面。三投影面兩兩相交產生的交線OX、OY、OZ 稱為三根投影軸,簡稱X 軸、Y 軸、Z 軸(如右圖),三軸的交點O 稱為原點。
二、點的三面投影
空間一點A 在三面投影體系中分別向三個投影面H、V、W作投射線,投射線在H面、V面、W面的垂足a、a'、a"稱為點A 的三面投影(如右圖)。圖中每兩條投射線分別確定一個平面,它們與三根投影軸分別交於ax,ay和az。
約定:空間點用大寫字母表示,例如A;投影用相應的小寫字母表示,例如水平投影a;正面投影用相應的小寫字母帶“'”表示,例如a'; 側面投影用相應的小寫字母帶“"”表示,例如a"。
三、點的投影圖
V 面不動,H 面和W 面沿OY 軸分開而形成OYH 和OYW,水平面H 和水平投影一起繞OX 軸往下旋轉與正面V 重合;側面W 連同側面投影一起繞OZ 軸往右旋轉與正面V 重合得到展開后的投影圖(如圖(b))。在點的投影圖中一般不畫出投影面的邊界線,也不標出投影面的名稱。常見的點的投影圖如圖(c)。
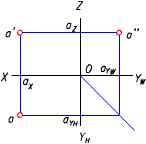
(a)點A的三面投影及其展開(b)H面、W面轉到與V面重合(c)點的投影圖
四、點的投影規律
由下圖可見:Aa = a'ax = a"ay = z 坐標,反映點A 到H 面的距離;Aa' = aax = a"az = y 坐標,反映點A 到V 面的距離;Aa" = aay = a'az = x 坐標,反映點A 到W 面的距離。同時有:a'a 垂直於OX 軸,a'a" 垂直於OZ 軸,aa" 垂直於OY 軸。
點的三面投影規律為:
1、兩面投影連線垂直於相應的投影軸;
2、點的投影到投影軸的距離等於該點到相應投影面的距離,等於該點的相應坐標。
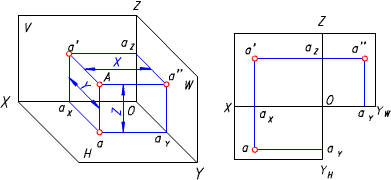
(a)點在三面投影體系中的投影(b)展開圖
空間點A到三個投影面的距離Aa"、Aa'、Aa可用點A的三個直角坐標xA、yA和zA表示,記為(xA,yA,zA)。
例3-1 已知空間點A(11,8,15),求作它的三面投影圖。
例3-2 如下圖所示,已知空間點B 的正面投影b′和水平投影b,求作該點的側面投影b″。
分析: 由點的投影規律可知:b′b″⊥ 0Z 軸,所以 b″一定在過b′且垂直於OZ軸的直線上,又因b到OX軸的距離bbx等於b″到OZ軸的距離b″bz,利用此關係,便可以求得b″。
3.2.2 兩點的相對位
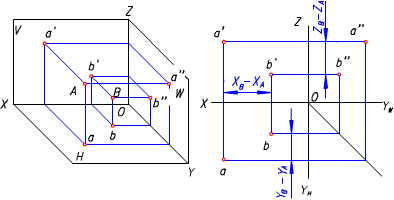
如圖(a)所示,有A、B 兩個點,它們對投影面的相對位置確定了A、B 兩點各自的坐標,而A、 B 兩點間的相對位置是由各方向的坐標差來決定的。 如圖(b)所示,設點A 和點B 的坐標分別為(XA、YA、ZA)和(XB、YB、ZB),如以點A 為基準點,當點B 與它比較時,則點B 對點A 的一組坐標差為:
△X(X軸方向坐標差)=XB-XA,確定兩點左、右相對位置; △Y (Y 軸方向坐標差)=YB-YA,確定兩點Z(Z軸方向坐標 差)=ZB-ZA,確定兩點上、下相對位置。 △X、△Y、△Z為正時,點B 分別在基準點A 的左方、前方、上方; △X、△Y、△Z 為負時,點B 分別在基準點A 的右方、後方、下方。
例3-3 已知點A 的三面投影a 、a′、a″,如圖所示,並知點B 在點A 左方11mm,在點A 上方8mm,在點A 前方6mm,求作點B 的三面投影b、b′、b″ 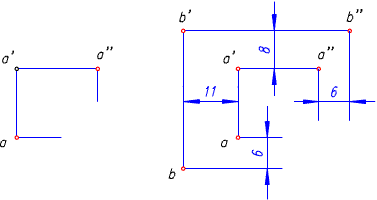
圖中省去了坐標軸,故稱為無軸投影圖。這是由於在畫物體的三面投影時,往往是利用相對坐標作圖,從而省去坐標軸。工程圖樣基本上都是使用這種無軸投影圖。
3.2.3 重影點
一、重影點的概念
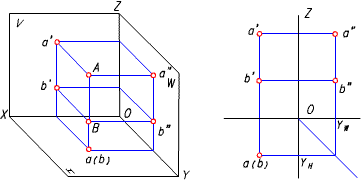
如果空間兩點位於某一投影面的同一條投射線上,則這兩點在該投影面上的投影就會重合為一點,稱之為對該投影面的重影點。如圖,A、B 兩點的X、 Y 坐標相等,而Z 坐標不等,從而它們的水平投影重合為一點,稱之為對H 面的重影點。 類似地,也會有V 面重影點和W 面重影點。
二、重影點的作用
利用重影點可以判別兩點的可見性。對於某面重影點,規定距該面距離較遠,即坐標值大者為可見。反之,為不可見。如圖,因為ZA>ZB,故水平投影上a 可見,b 不可見,對不可見點的投影加上括弧。
3.2.4 直線的投影
直線是無限長的。直線的空間位置可由線上兩點確定。直線上兩點之間的線段稱為直線段。為了敘述方便,本課程把直線段簡稱為直線。直線的投影可由線上兩點在同一個投影面上的投影(同面投影)相連而得。例如,要作出直線AB的三面投影,可先作出其兩端點a、a’、a” 和b、b'、b",如圖(a)所示,然後將其同面投影相連,即得AB直線的三面投影ab、a'b'、a"b",如圖(b)所示。 直線與投影面的夾角稱為直線對投影面的傾角。其對H面的傾角用a表示,對V面的傾角用b 表示,對W面的傾角用g表示。
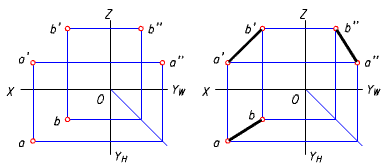
(a) 兩點的投影(b) 直線的投影
3.2.5 投影面平行線
平行於某一投影面,同時傾斜於另外兩個投影面的直線稱為投影面平行線。
一、水平線
平行於水平面的直線稱為水平線。水平線的投影特性:
1) 它的水平投影反映實長,即ab = AB;
2) 它的正面投影a'b' 平行於X軸,側面投影a"b" 平行於OYW 軸;
3) 它的水平投影與X 軸的夾角等於該直線對V 面的傾角b,與OYH 軸的夾角等於該直線對W 面的傾角g。
二、正平線
平行於正面的直線稱為正平線。正平線的投影特性:
1) 它的正面投影反映實長,即a'b' = AB;
2) 它的水平投影ab 平行於X 軸,側面投影a"b" 平行於Z 軸;
3) 它的正面投影與X 軸的夾角等於該直線對H 面的傾角a,與Z 軸的夾角等於該直線對W 面的傾角g。
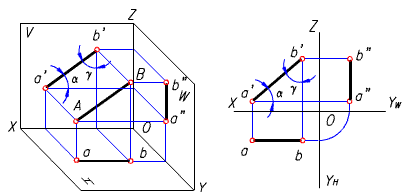
(a) 直觀圖 (b) 投影圖
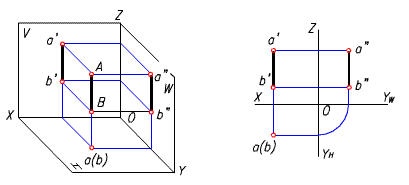
三、側平線
平行於側面的直線稱為側平線。側平線的投影特性:
1) 它的側面投影反映實長,即a"b" = AB;
2) 它的水平投影ab 平行於OYH 軸,正面投影a'b' 平行於Z 軸;
3) 它的側面投影與OYW 軸的夾角等於該直線對H 面的傾角a,與Z 軸的夾角等於該直線對V 面的傾角b。
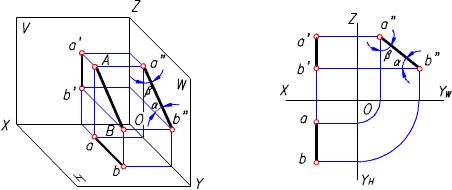
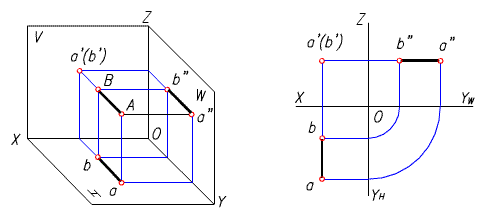
二、正垂線
垂直於正面的直線稱為正垂線。正垂線的投影特性:
1) 它的正面投影積聚為一點,即a'(b');
2) 它的另外兩個投影都垂直於相應的投影軸,且反映線段的實長,即ab 垂直於OX 軸,a"b" 垂直於OZ 軸,ab = a"b" = AB。
三、側垂線
垂直於側面的直線稱為側垂線。側垂線的投影特性:
1) 它的側面投影積聚為一點,即a"(b");
2) 它的另外兩個投影都垂直於相應的投影軸,且反映線段的實長,即ab 垂直於OYH 軸,a'b' 垂直於OZ 軸,ab = a'b' = AB。
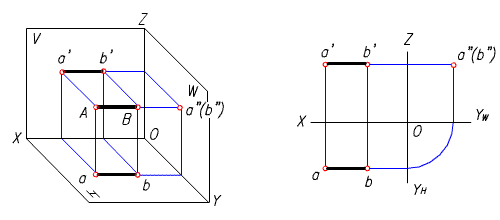
(a) 直觀圖 (b) 投影圖