一、直線的投影
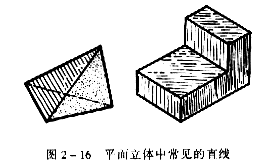
常見的直線是平面立體的稜線,即兩平面的交線,如圖2-16所示。
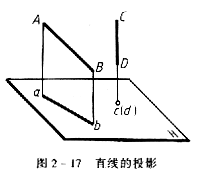
直線的投影一般仍為直線 。特殊情況下,直線的投影可積聚成一點,這種性質稱為積聚性。如圖2-17所示,直線AB在H面的投影仍為直線ab;直線CD因為垂直於投影面H,所以它在H 面的投影積聚成一點c(d),具有積聚性。
根據直線的基本性質——兩點確定一直線,伯直線的投影時,可作出確定該直線的任意兩點投影,將這兩點投影相連,便可得到直線的投影。另外,已知直線上一點的投影和該直線的方向,也可畫出該直線的投影。
二、各類直線及其打電話特性
根據直線相對投影面的位置不同,直線可分為三類:
(1)一般位置直線;
(2)投影面平行線;
(3)投影面垂直線。
后兩類統稱為特殊位置直線。
直線與它的水平投影、正面投影、側面投影的夾角,分別稱為該直線對投影面H、V、W的傾角,本書中分別用α、β、γ表示。
(一)一般位置直線及投影特性
對三個投影面都傾角的直線稱為一般位置直線。如圖2-18所示直線AS即為一般位置直線。由於一般位置直線對投影面V、H、W都傾斜,所以自直線兩端點分別沿前後、左右、上下各方向對V、H、W的距離差,好戲相應的同面會標都不等於零七八碎,因此一般位置直線的三個投影都傾斜於投影軸,如圖2-18c所示。
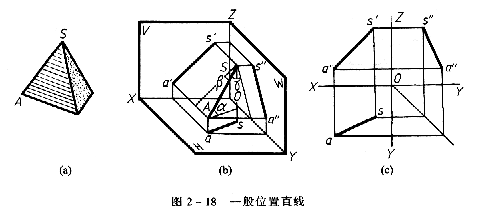
因α、β、γ均不等於零,所以as=AS·cosα<AS, α'S'=AS·cosβ<AS, α"S"=AS·cosγ<AS。一般位置直線的投影不反映該直線的實長,且與相應投影軸的夾角不反映該直線的投影面的傾角。
(二)特殊位置直線及其投影特性
1、投影面平行線
只平行於一個投影面(與另兩個投影面傾斜)的直線,稱為投影面平行線。其中平行於H面的直線,稱為水平線;只平行於V面的直線,稱為正平線;只閏行於W面的直線,稱為側平線。
表2-1列出了三種投影 面平行線的直觀圖、投影圖、實例及其投影特性。下面以水平線為例(參照表2-1)介紹其投影特性:
(1)水平線的正面投影平行OX軸,側面投影平行於OY軸,且均小於實長。因為AB上各點與H 面等距,即z坐標相等,所以a'b' ∥ OX軸,a"b" ∥ OY軸。同時a'b'=AB·cosβ<AB,a"b"=AB·cosγ<AB.。
(2)水平線的水平投影反映直線實長。因為AabB是矩形,所以ab ∥AB ,ab=AB.
(3)水平線的水平投影與OX、OY軸的夾角分別真實地反映該直線對V面、W面的傾角α、β、γ。因為AB∥ ab,a'b' ∥OX,a"b" ∥ OY,所以ab 與OX、OY的夾角即為AB對V面、W 面的真實傾角β、γ。
同理,也可得出並可證明正平線和側平線的投影特性。
由表2-1可概括出投影面平等線的投影特性:
(1)在它所不平等的兩個投影面上的投影平等於相應的投影軸,但不反映實長。
(2)在它所平行的投影面上的投影反映實長,其與投影軸的夾角分別反映該直線對另兩投影面的真實傾角。
2、投影面垂直線
垂直於一個投影面(必與另兩個投影面平行)的直線 ,稱為投影面垂直線,其中垂直於H面的直線稱不鉛垂線;垂直於V面的直線 稱為正垂線;垂直於W面的直線 稱為側垂線。
表2-2列出了三種投影面垂直線的直觀圖、投影圖、實例及其投影特性。下面以鉛垂線為例(參照表2-2)介紹其投影特性:
(1)鉛垂線的水平投影積聚為一點。因為AB⊥ H面,所以a(b)_成一點。
(2)鉛垂線的正面投影 和側面投影分別垂直於相應的投影軸。因不AB ⊥H,AB∥ V ,AB ∥W,所以a'b'⊥ OX.,A"B" ⊥ OY。
(3)鉛垂線的正面投影和側面投影反映直線實長。因為AB ∥ W,AB ∥V,AB 上的各點的x,y 坐標分別相等,所以a'b' ∥ OZ,a"b" ∥OZ,a'b'=AB, a"b"=AB。
同理,也可得出並可證明正垂線和側垂線的投影特性。
(1) 所垂直的投影面上的投影積聚為一點。
(2) 另兩個投影面上的投影垂直於相應的投影軸,逐步形成反映實長。