兩直線的相對位置除上述情況之外,還有一種情況有必要討論因為它是處理一自然風光垂直問題睥基礎作圖經常會遇到,即一邊平行投影面的直角投影定理。
一、直線平行投影面的垂直相交兩直線的投影
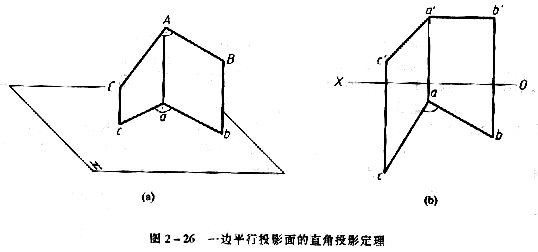
垂直相交的兩直線,當其中一條直線為投影面平行線時,則兩直線在該投影同上的投影也必定互相垂直。反之,若相交兩直線在某一投影面上的投影互相垂直且其中有一條直線為該投影面的平行線,則這兩直線在空間也必定互相垂直。
如圖2—26a、b所示,設相交兩直線AB⊥AC且AB∥H面。顯然,直線AB垂直於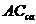 (因為
(因為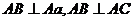 )。今ab∥AB,則ab⊥平面AacC,因此,ab⊥ac,亦即∠bac=
)。今ab∥AB,則ab⊥平面AacC,因此,ab⊥ac,亦即∠bac=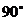 。
。
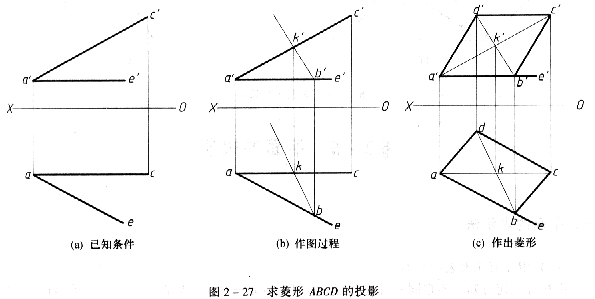
[例2—5] 如圖2—27所示,已知一菱形ABCD的一條對角線AC,以及菱形的一邊AB位於直線AE上,求該菱形的投影。
分析菱形的兩對角線互相垂直,且交點平分對角線的線長度。
作圖步驟(如圖2—27b、c所示):
(1)在對角線AC上取中點K,K點也必定是另一對角線的中點。
(2)AC是正平線,故另一對角線的正面投影垂直於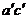 。先過
。先過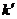 作
作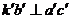 ,並與
,並與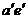 交於
交於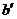 ,由
,由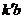 求出kb.
求出kb.
(3)在對角線KB的延長線上取一點D,使KB=KD(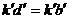 ,kd=kb),則
,kd=kb),則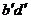 和bd即為另一對角線的投影。連接各頂點A、B、C、D的同面投影,即得菱形ABCD的兩面投影。
和bd即為另一對角線的投影。連接各頂點A、B、C、D的同面投影,即得菱形ABCD的兩面投影。
二、一直線平行投影面的交叉垂直兩直線的投影
上述定理可推廣到交叉成直角的兩直線的投影情況。
垂直交叉的兩直線,當其中一條直線為投影面平行線時,則兩直線在該投影面上的投影也必定互相垂直。反之,若交叉兩直線在某一投影面上的投影互相垂直,且其中有一條直線為該投影面的平行線,則這兩直線在空間也必定互相垂直。
如圖2—28a、b所示,設交叉兩直線AB⊥MN,且AB∥H面,MN不平行H面。證明見圖2—28a;過直線AB上任意點A作直線AC∥MN,則AC⊥AB。由一直線平行投影面的垂直相交兩直線的投影特性可知;ab⊥ac,今AC∥MN,則其投影ab∥mn,故ab⊥mn