直線的投影變換,有下述三種情況。
一、將一般位置直線變換為投影面平行線
因為與一般位置直線相平行的平面可以為一般位置平面或投影面垂直面,而處於投影面垂直面位置的平面可作為新投影面與被保留的舊投影面相垂直,構成新的兩投影面體系,所以將一般位置直線變換為投影面平行線只需一次換面。其牡丹通常為求一般位置直線的實長、其對投影面的傾角及方便求解度量和定位問題。
如圖3-6所示,將一般直線變換為V 面的平行線,為了使AB在H/ V
面的平行線,為了使AB在H/ V 體系中成為V
體系中成為V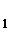 面的平行線,可以用一個既垂直於H面,又平行於AB的V
面的平行線,可以用一個既垂直於H面,又平行於AB的V 面替換V面,通過一次變換即可達到目的,按照V
面替換V面,通過一次變換即可達到目的,按照V 面平行線的投影特性,在H/ V
面平行線的投影特性,在H/ V 體系中新投影軸X
體系中新投影軸X 應平行於所保留的投影b a。
應平行於所保留的投影b a。
作圖步驟(如圖3-6b所示):
(1)在適當位置作X ∥a b(設置的新投影軸,應使幾何元素在新投影體系中的兩個投影分別位於新投影軸的兩側;新投影軸距離直線被保留的投影之間距離可任取)。
∥a b(設置的新投影軸,應使幾何元素在新投影體系中的兩個投影分別位於新投影軸的兩側;新投影軸距離直線被保留的投影之間距離可任取)。
(2)按投影變換的基本作圖法,分別求出線段AB 兩端點的新投影b′ 和a′
和a′ ,連b′
,連b′ 與a′
與a′ ,a′
,a′ b′
b′ 即為所求AB的V
即為所求AB的V 面投影。
面投影。
將一般位置直線變換為V 面的平行線,其作圖結果為:直線AB 在V
面的平行線,其作圖結果為:直線AB 在V 面上的投影a′
面上的投影a′ b′
b′ 反映其實長,且a′
反映其實長,且a′ b′
b′ 與X
與X 軸的夾角等於直線AB對H面的真實傾角α。
軸的夾角等於直線AB對H面的真實傾角α。
同理可將一般位置直線變換為H 面的平行線。通過一次換面,即可求得該直線實長和對V面的真實傾角β。
面的平行線。通過一次換面,即可求得該直線實長和對V面的真實傾角β。
由此可知:通過一次換面,可以將一般位置直線變換為新投影面的平行線。欲使新投影面平行於已知一般位置直線,則新投影軸應平行於該直線所保留的投影。作圖的關鍵是在空間確定新投影面的位置。而在投影圖上則是確定新投影軸的位置。
二、將投影面平行線變換為投影面垂直線
因為與投影面平行線相垂直的平面一定垂直於它所平行的那個投影面,因此,這樣的位置平面就可作為新投影面,與所垂直的被保留的投影面構成新的兩投影面體系,故將投影面平行線變換為投影面垂直線只需一次換面。其目的通常是為了方便求解某些度量和定位問題。
如圖3-7所示,將正平線變換為H 面的垂直線。因為在V/H體系中,垂直於正平線AB的平面也必垂直與V面,於是可用垂直於AB的正垂面為H
面的垂直線。因為在V/H體系中,垂直於正平線AB的平面也必垂直與V面,於是可用垂直於AB的正垂面為H 面來替換H面,使AB成為新體系V/H
面來替換H面,使AB成為新體系V/H 中的H
中的H 面垂直線。按照H
面垂直線。按照H 面垂直線的投影特性,在V/H
面垂直線的投影特性,在V/H 中新投影軸X
中新投影軸X 應垂直與被保留的反映實長的投影a′b′,直線AB在H
應垂直與被保留的反映實長的投影a′b′,直線AB在H 面上的投影a
面上的投影a b
b 必積聚為一點。
必積聚為一點。
作圖步驟(如圖3-7b所示):
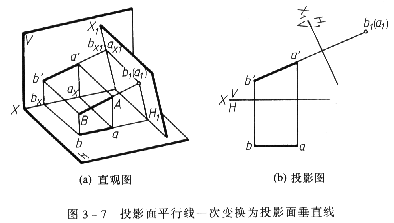
(1)在適當位置作X ⊥a′b′。
⊥a′b′。
(2)按投影變換的基本作圖法求得端點B和A的新投影b 和a
和a 必重合為一點,則a
必重合為一點,則a b
b 即為AB所求的H
即為AB所求的H 面投影。
面投影。
同理,也可通過一次換面將水平線變換為V 面的垂直線。
面的垂直線。
由此可知:通過一次換面,可以將投影面平行線變換為投影面垂直線,欲使新投影面垂直於已知的投影面平行線,則新投影軸應垂直於該直線所保留的反映實長的投影。
三、將一般位置直線變換為投影面垂直線
若選新投影面直接垂直於一般位置直線,則新投影面必定是一般位置平面,而它和原體系中的任一投影面都不垂直,不能構成新的兩投影面體系。所以欲使一般位置直線變換為投影面垂直線,只經一次換面是不行的。
由上述第一種基本情況和第二種基本情況可知,將一般位置直線變換為投影面垂直線,必須經兩次換面,先將直線變換為投影面平行線,再將投影面平行線變換為投影面垂直線。
圖3-8a、b為一般位置直線經兩次換面,變換為投影面垂直線的直觀圖和投影圖。
作圖步驟(如圖3-8b所示):
(1)先將AB變換為V 面的平行線 作法與圖3-6b相同,即作X
面的平行線 作法與圖3-6b相同,即作X ∥a b,將V/H中的a′b′變換為V
∥a b,將V/H中的a′b′變換為V /H中的a′
/H中的a′ b′
b′ 。a′
。a′ b′
b′ 即為AB的V
即為AB的V 面投影。
面投影。
(2)再將AB變換為H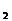 面的垂直線 作法與圖3-7b相同,即作X
面的垂直線 作法與圖3-7b相同,即作X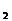 ⊥a′
⊥a′ b′
b′ ,將V
,將V /H中的a b變換為V
/H中的a b變換為V /H
/H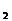 中的b
中的b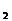 (a
(a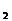 ),b
),b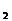 (a
(a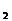 )積聚為一點,即為AB的H
)積聚為一點,即為AB的H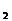 面的投影。於是V/H中的一般位置直線AB就變換為V
面的投影。於是V/H中的一般位置直線AB就變換為V /H
/H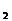 中的H
中的H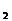 面垂直線。
面垂直線。
同理,也可先將直線AB變換為H 面平行線,再將AB變換為V
面平行線,再將AB變換為V 面的垂直線。
面的垂直線。
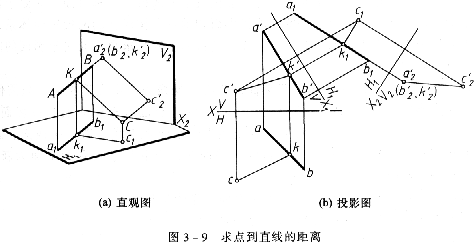
如圖3-9所示,求點C到直線AB的距離。
分析: 點到直線的距離,即為過點作直線的垂線,求出垂足,點與垂足間的這段垂線的實長。作點C到直線AB的垂線CK,當直線AB為某一投影面的平行線時,則AB與CK在該投影面上的投影反映垂直(正交),但此時的垂線CK仍為一般位置直線,不反映實長。而當直線AB為投影面的垂線時,CK為該投影面的平行線,點C到直線的距離CK在直線AB所垂直的投影面上的投影c′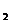 (k′
(k′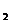 )才是實長的真實反映。故此題求點至一般位置直線的距離,須經兩次換面,將一般位置直線AB變換為投影面垂直線,點C隨之變換,既可解決,此時,在第二換面的新投影面上,直線AB的積聚投影(點)與點C的同面投影之間的距離,既為所求的點C到直線AB的距離。圖3-9a只示出了第二次換面時的空間分析。
)才是實長的真實反映。故此題求點至一般位置直線的距離,須經兩次換面,將一般位置直線AB變換為投影面垂直線,點C隨之變換,既可解決,此時,在第二換面的新投影面上,直線AB的積聚投影(點)與點C的同面投影之間的距離,既為所求的點C到直線AB的距離。圖3-9a只示出了第二次換面時的空間分析。
作圖步驟(如圖3-9b所示):
(1)先將直線AB變換為H 面的平行線,AB在H
面的平行線,AB在H 面上的投影為a
面上的投影為a b
b ;點C也隨之變換,在H
;點C也隨之變換,在H 面上的投影為c
面上的投影為c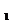 。
。
(2)再將直線AB變換為V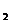 面的垂直線,AB在V
面的垂直線,AB在V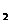 面上的投影積聚為一點a
面上的投影積聚為一點a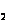 ′(b
′(b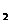 ′);點C在V
′);點C在V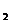 面上的投影為c
面上的投影為c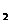 ′。c
′。c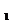 作c
作c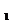 k
k ⊥a
⊥a b
b ,即c
,即c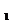 k
k ∥X
∥X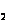 軸得k
軸得k ,k
,k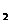 ′
′
(3)在V/ H 中,按一邊平行投影面的直角投影定理,過與a
中,按一邊平行投影面的直角投影定理,過與a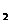 ′(b
′(b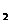 ′)重影,連接c
′)重影,連接c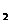 ′、k
′、k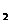 ′,c
′,c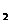 ′k
′k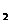 ′即反映點C到直線AB的距離。
′即反映點C到直線AB的距離。
如要求出CK在V/H體系中的投影c′k′和ck,可根據c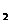 ′k
′k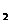 ′、c
′、c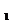 k
k 返回作出。
返回作出。