由於平面立體的表面四有若干個多邊形平面所圍成,因此,繪製平面立體的投影可歸結為回子它的各表面的投影。平面立體各表面的交線稱為稜線。平面立體的各表面是由稜線所圍成,而每條稜線可由其兩端點確定,因此,繪製平面立體的投影可歸結為繪製各稜線及各頂點的投影。作圖時,應判別其可見性,把可見稜線的投影畫成粗實線,不可見稜線的投影畫成虛線。
一、稜柱
(一)稜柱的投影
圖4—1所示為一正放(立體的表面、對稱平面、迴轉軸線相對於投影面處於平行或垂直的位置)的正六稜柱直觀圖及投影圖。正六稜柱由頂面、底面和六個側棱面圍成。頂面、底面分別由六條底稜線圍成(正六邊形);每個側棱面又由兩條側稜線和兩條低稜線圍成的(矩形)。
1.投影分析
(1)正六稜柱的頂面、底面 均為水平面,其水平投影反映頂面、底面的真形,且互相重合;正面投影和側面投影均積聚為平行於相應投影軸的直線。
(2)六個側棱面 其前後兩個棱面為正平面,其水平投影重合,且反映真形;水平投影和側面投影都積聚成平行於相應軸的直線。其餘四個側棱面都為鉛垂面,其水平投影分別積聚成傾斜直線;正面投影和側面投影均為類似形(矩形),且兩側棱面投影對應重合。由於六個側棱面的水平投影均有積聚性,故與頂面、底面邊線(底稜線)的水平投影重合。
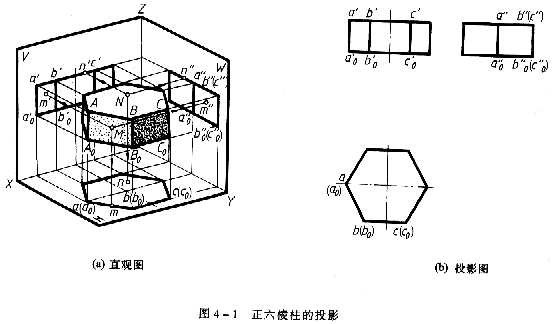
(3)稜線 頂、底面各有六條底稜線,其總前、后兩條為側垂線,四條為水平線;而六條側稜線均為鉛垂線。它們的三面投影,請讀者自行分析。
2.作圖步驟
畫正放稜柱(如正六稜柱)的投影圖時,一般先畫出對稱中心線,對稱線,再畫出稜柱水平投影(如正六邊形);然後根據投影關係畫出它的正面投影和側面投影。應注意當稜線投影與對稱重合(如圖中稜線AAo側面投影a〃a〃o)時應畫成粗實線.
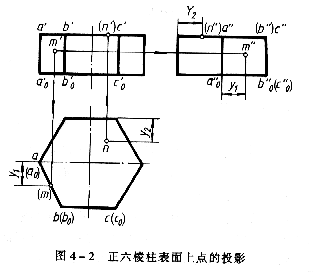
(二)稜柱表面上取點
在平面立體表面上取點,其原理和方法與平面上取點相同,由於正放稜柱的各個表面都處於特殊位置,因此,在其表面上取點均可利用平面投影積聚性作圖,並表面可見性.例如,在增六稜柱表面上有一點M,已知其正面投影m〃,要作出水平和側面投影(圖4—2).由於點M的正面投影是可見的,所以點M必定的左前方的AaoBoB上(參閱4—1a).而該棱面的鉛垂面,因此點M的水平投影m必在該棱面有積聚性的水平投影aa%b b直線上,再根據投影關係由m’和(m)求出m’.由於棱面AAoBoB處於左前方,側面投影可見,所以其上的點M的側面投影也可見,它的水平投影(m)不可見。又如,已知點N的水平投影n,求n’和n〃.由於n可見,所以點N必定在頂面上,而頂面為水平面,其正面投影和側面投影都具有積聚性.因此,(n’)、(n〃)也必分別在頂面的正面投影和側面投影所積聚的直線上,均不可見。
二、稜錐
(一)稜錐的投影
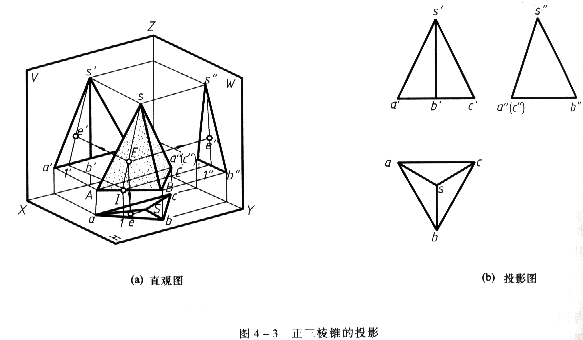
圖4—3所示為一正放的正三稜錐直觀圖及投影圖。正三稜錐有地面和三個側棱面圍成。底面又由三條稜線圍成(正三角形),三個側棱面由三條側稜線和三條底稜線圍成(三個真形大小相等的等腰三角形)。
1.投影分析
(1)正三稜錐底面△ABC為水平面,其水平投影△a b c反映真形,正面投影和側面投影均積聚為平行於相應投影軸的直線a′b′c′和a〃(c〃)b〃。
(2)三個側棱面中的左右兩個側棱面△SAB和△SBC為一般位置平面,其三面投影均不反映真形,且側面投影重合。
(3)后側棱面△SAC為側垂面(因含側垂線AC),其側面投影積聚成斜向直線s〃a〃(c〃),正面投影△s′a′c′和水平投影△sac均不反映真形,且正面投影△s′a′c′與△s′a′b′、△ s′b′c′重合。
(4)三個側棱面△SAB、△SBC、△SCA的水平投影△s a b、△s b c、△s c a與底面△ABC的水平投影△a b c重合。
(5)底面的三條底稜線中有兩條是水平線AB和BC,一條是側垂線AC;而三條側冷縣總,有兩條是一般位置直線SA和SC,一條是側平線SB,它們的三面投影,請讀者自行分析。
2.作圖步驟
畫正放的正三稜錐的投影圖是哦,一般可先畫出底面的水平投影(正三角形)和底面的另兩個投影(均積聚為直線);再畫出錐頂的三個投影;然後將錐頂和底面三個頂點的同面投影連接起來,即得正三稜錐的三面投影。也可先畫出三稜錐(底面和三個側棱面)的一個投影(如水平投影),再依照投影關係畫出另兩個投影。
(二) 稜錐表面上取點
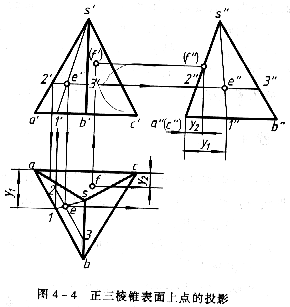
在稜錐表面上取點,其原理和方法與在平面上取點相同,如果點在立體的特殊平面上,則可利用該平面投影有積聚性作圖;如果點在立體的一般位置平面上,則可利用輔助線作圖,並表明可見性。如圖4—4所示,並參閱圖4—3a,在正三稜錐表面上有一點E,已知其正面投影e’,要作出e和e〃。其作圖原理與在平面上取點時相同。由於e可見,所以點E在左棱面△SAB(一般位置平面)上,欲求點E的另兩個投影e、e〃,必須利用輔助線作圖,具體方法可有以下三種:
(1)過點E和錐頂作輔助直線s I,其正面投影s′I′必通過e’;求出輔助線sI的水平投影s I和側面投影s〃I〃,則點E水平投影e必在s I上,側面投影也必在s〃I〃上。
(2)也可過點E作底棱AB的平行線ⅡⅢ,則2’3’//a’b’且通過e’,求出ⅡⅢ的水平投影(23//ab,必通過e)和側面投影(2〃3〃//a〃b〃,也必通過e〃).
(3)也可過欲求點在該點所在的棱面上作任意直線.先求出該輔助直線的投影,再求出點的投影(為使圖形清晰,圖中未示出).
由於側棱面△SAB處於左方,側面投影可見,故其上的點E的側面投影e〃水平投影e也可見.又如已知點F的水平投影f,求f’和f〃.由於f可見,所以知點F是在後棱面△SAC上,而不是在底面△ABC上.側棱面△SAC是側垂面,其側面投影具有積聚性,故f〃可利用積聚性直接求出,即(f〃)必在s〃a〃(c〃)直線是行,再由f和(f〃)求處(f’).由於側棱面△SAC處於後方,正面投影不可見,故其上的點F的正投影(f〃)不可見,側面投影(f〃)也不可見.