第二章 帶式輸送機摩擦傳動理論
一、摩擦傳動理論
帶式輸送機所需的牽引力是通過驅動裝置中的驅動滾筒與輸送帶間的摩擦作用而傳遞的,因而稱為摩擦傳動。為確保作用力的傳遞和牽引構件不在驅動輪上打滑,必須滿足下列條件:
(1)牽引構件具有足夠的張力;
(2)牽引帶與驅動滾筒的接觸表面有一定的粗糙度;
(3)牽引帶在驅動輪上有足夠大的圍包角。
圖l—22為一台帶式輸送機的簡圖。當驅動滾筒按順時針方向轉動時,通過它與輸送帶間的摩擦力驅動輸送帶沿箭頭方向運動。


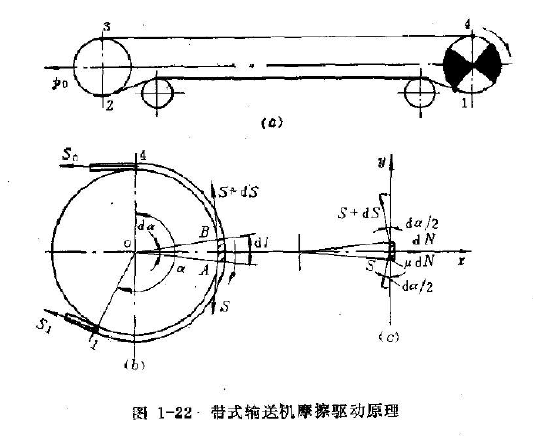
在輸送帶不工作時,帶子上各點張力是相等的。當輸送帶運動時,各點張力就不等了。其大小取決於張緊力P0、運輸機的生產率、輸送帶的速度、寬度、輸送機長度、傾角、托輥結構性能等等。故輸送帶的張力由l點到4點逐漸增加,而在繞經驅動滾筒的主動段,由4點到l點張力逐漸減小。必須使輸送帶在驅動滾筒上的趨入點張力Sn大於奔離點張力S1,方能克服運行阻力,使輸送帶運動。此兩點張力之差,即為驅動滾筒傳遞給輸送帶的牽引力W0。在數值上它等於輸送帶沿驅動滾筒圍包弧上摩擦力的總和,即
W0=Sn-S1 (1—1)
趨入點張力Sn隨輸送帶上負載的增加而增大,當負載過大時,致使(Sn-S1)之差值大於摩擦力,此時輸送帶在驅動滾筒上打滑而不能正常工作。該現象在選煤廠中可經常遇到。
Sn與S1應保持何種關係方能防止打滑,保證輸送帶正常工作,這是將要研究的問題。
在討論前,先作如下假設:
(1)假設輸送帶是理想的撓性體,可以任意彎曲,不受彎曲應力影響;
(2)假設繞經驅動滾筒上的輸送帶的重力和所受的離心力忽略不計(因與輸送帶上張力和摩擦力相比數值很小)。
如圖l—22b所示,在驅動滾筒上取一單元長為dl的輸送帶,對應的中心角即圍包角為dα。當滾筒迴轉時,作用在這小段輸送帶兩端張力分別為S及S+dS。在極限狀態下,即摩擦力達到最大靜摩擦力時,dS應為正壓力dN與摩擦係數μ的乘積,即
dS=μdN
dN為滾筒給輸送帶以上的作用力總和。
列出該單元長度輸送帶受力平衡方程式為
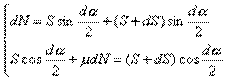
由於dα很小,故sin(dα/2)≈(dα/2),cos(dα/2)≈1,上述方程組可簡化為
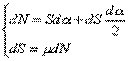
略去二次微量:dSdα,解上述方程組得 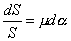 .
.
通過在這段單元長度上輸送帶的受力分析,可以得到,當摩擦力達到最大極限值時,欲保持輸送帶不打滑,各參數間的關係應滿足dS/S=μdα。以定積分方法解之,即可得出輸送帶在整個驅動滾筒圍包弧上,在不打滑的極限平衡狀態下,趨入點的Sn與奔離點的Sk之間的關係
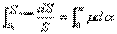
解上式,得 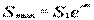
式中 e——自然對數的底,e=2.718;
μ——驅動滾筒與輸送帶之間的摩擦係數;
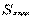 ——輸送帶在驅動滾筒上趨入點的最大張力;
——輸送帶在驅動滾筒上趨入點的最大張力;
S1一一輸送帶在驅動滾筒奔離點的張力;
α——輸送帶在驅動滾筒上的圍包角,弧度。
上式)即撓性體摩擦驅動的歐拉公式。根據歐拉公式可以繪出在驅動滾筒圍包弧上輸送帶張力變化的曲線,見圖l—23中的bca''。
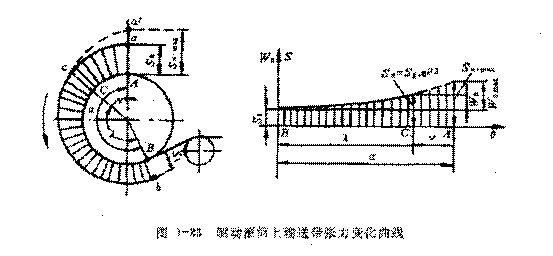
從上述分析可知,歐拉公式只是表達了趨入點張力為最大極限值時的平衡狀態。
而實際生產中載荷往往是不均衡的;而且,在歐拉公式討論中,將輸送帶看作是不變形的撓性體,實際上輸送帶(如橡膠帶)是一個彈性體,在張力作用下,要產生彈性伸長,其伸長量與張力值大小成正比。因此,輸送帶沿驅動滾筒圓周上的分佈規律見圖1—23中bca曲線變化(而不是bca’)。在BC弧內,輸送帶張力按歐拉公式之規律變化;到c點后,張力達到Sn值,在CA弧內,Sn值保持不變。也就是說為了防止輸送帶在驅動滾筒上打滑,應使趨入點的實際張力Sn小於極限狀態下的最大張力值,即
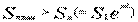
既然輸送帶是彈性體,那麼,在受力后就要產生彈性伸長變形。這是彈性體與剛性體最本質的區別。受力愈大,變形也愈大,而輸送帶張力是由趨入點向奔離點逐漸減小,即在趨入點輸送帶被拉長的部分,在向奔離點運動過程中,隨著張力的減小而逐漸收縮,從而使輸送帶與滾筒問產生相對滑動,這種滑動稱為彈性滑動或彈性蠕動(它與打滑現象不同)。顯然,彈性滑動只發生於輸送帶在驅動滾筒圍包弧上有張力變化的一段弧內。產生彈性滑動的這一段圍包弧,稱為滑動弧,即圖l-23中的BC弧,滑動弧所對應的中心角稱為滑動角,即λ角;不產生彈性滑動的圍包弧,稱為靜止弧(圖中的CA弧),靜止弧所對應的中心角,稱為靜止角,即圖中γ角。滑動弧兩端的張力差,即為驅動滾筒傳遞給輸送帶的牽引力。由此可見,只有存在滑動弧,驅動滾筒才能通過摩擦將牽引力傳遞給輸送帶;在靜止弧內不傳遞牽引力,但它保證驅動裝置具有一定的備用牽引力。
當輸送機上負載增加時,趨入點張力Sn增大,滑動弧及對應的滑動角也相應均要增大,而靜止弧及靜止角則隨之減小。圖1—23中的C點向A點靠攏,當趨入點張力Sn增大至極限值Snmax時,則整個圍包弧BA弧都變成了滑動弧,即C點與A點重合,整個圍包角都變成了滑動角(λ=α,γ=0)。這時驅動滾筒上傳送的牽引力達到最大值的極限摩擦力:
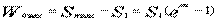 (1—4)
(1—4)
若輸送機上的負荷再增加,即 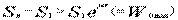 ,這時.輸送帶將在驅動滾筒上打滑,輸送機則不能正常工作。
,這時.輸送帶將在驅動滾筒上打滑,輸送機則不能正常工作。
二、提高牽引力的途徑
根據庫擦傳動的理論及式(1—4)均可以看出,提高帶式輸送機的牽引力可以採用以下三種方法:
(1)增加奔離點的張力S1,以提高牽引力。具體的措施是通過張緊輸送機的拉緊裝置來實現。隨著S1的增大,輸送帶上的最大張力也相應增大,就要求提高輸送帶的強度,這種做法是不經濟的,在技術上也不合理。
(2)改善驅動滾筒表面的狀況,以得到較大的摩擦係數μ,由表1—29可知,膠面滾筒的摩擦係數比光面滾筒大,環境乾燥時比潮濕時大,所以,可以採用包膠、鑄塑,或者採用在膠面上壓制花紋的方法來提高摩擦係數。
(3)採用增加輸送帶在驅動滾筒上的圍包角來提高牽引力。其具體措施是增設改向滾筒(即增面輪)可使包角由180°增至210°-240°必要時採用雙滾筒驅動。
三、剛性聯繫雙滾筒驅動牽引力及其分配比朗確定
剛性聯繫雙滾筒和單滾筒相比,增加一個主動滾筒:當兩個滾筒的直徑相等時其角度是相同的(圖1—24)。從圖l—24中可以看出,輸送帶由滾筒②的C點到滾筒①
的B點時,這兩點之間除了一小段(BC段)膠帶的臼重外,張力沒有任何變化,故B點可看作C點的繼續。因而剛性聯繫的雙滾筒與單滾筒實質上是相同的,因為滑動弧隨著張力增大而增大這一規律對它同樣適用的。
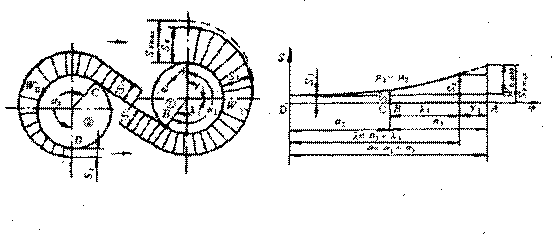
S1及μ值在一定的情況下,而且μl=μ2,只有當滾筒②傳遞的牽引力達到極限值時,滾筒①才開始傳遞牽引力。設λ1、λ2、γ1、γ2、α1、α2分別為第①及第②滾筒的滑動角,靜止角及圍包角、則在λ2=α2,λ1=0的情況下,靜止弧僅存在於滾筒①上。當λ2=α2時,λ1=α1-γ1時,輸送帶在兩個主動滾筒上張力變化曲線如圖1—24所示。
滾筒②可能傳遞的最大牽引力為
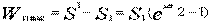
滾筒①可能傳遞的最大牽引力為
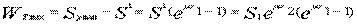
式中 S’——兩滾筒間輸送帶上的張力。
驅動裝置可能傳遞總的最大牽引力為
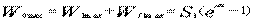
式中 α——總圍包角 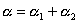
兩滾筒可能傳遞的最大牽引力之比為
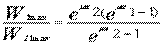
在一般情況下: 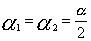 因而
因而
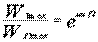 (1-5)
(1-5)
顯然,當第①滾筒上傳遞的牽引力未達到極限時,即 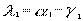 時,則兩驅動滾筒傳遞的牽引力之比為
時,則兩驅動滾筒傳遞的牽引力之比為
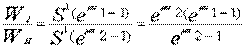
由上式可知,當總的牽引力W0和張力S1一定時,若μ值增加,則第⑧個驅動滾筒傳遞的牽引力WII增大,而WI減小。反之,若μ值減小時,則WI增大(因W0=WI+WII為一定值)。
由此可以看出:剛性聯繫的雙滾筒驅動裝置,其滾筒牽引力的分配比值隨摩擦係數的變化而改變。但由式(1-5)可知,驅動滾筒①可能傳遞的最大牽引力等於滾筒⑨的 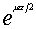 倍這一比值是不變的。
倍這一比值是不變的。
剛性聯繫的雙驅動滾筒缺點是已設計的牽引力分配比值,只適用於一定的荷載和一定的摩擦係數。當荷載變化,其比例也就被破壞了。此外,還由於大氣潮濕程度的變化,兩滾筒的表面清潔程度的不同,摩擦係數也發生了變化,其分配比實際上不可能保持定值。